In this tutorial we will discuss how to decide whether a perticular grammar/langauge is regular or not.
So follow given steps:

1. Every finite language is regular that means if there is a limit to the language then it is regular.
   For example the language, L = { a²⁰b²⁰} is regular langauge whereas,
   Langauge, L = { aⁿbⁿ| n > 0} is not regular.
2. Second case is if there is an infinite languge then we will check whether its DFA can be created. If no then it will not be a regular language
   And also we must have a pattern in the language otherwise FA cannot be created.
   

   ---

   Example
   Suppose given language, L = {ab, abab, ababab, ....}
   As we can see that there is a pattern in the language that is (ab)ⁿ
   So we can create FA for it as follows
   
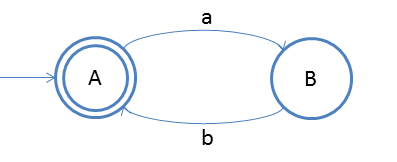
   Cleary it is NFA so we are good to say that the language given is a regular language.

   ---

3. String length should be in arithmetic progression