DPDA for aⁿbⁿc^m n,m≥1

Approch is quite similar to previous example, we will do just one add on for c^m.
First we have to count number of a's and that number should be equal to number of b's.
That we will achieve by pushing a's in STACK and then we will pop a's whenever "b" comes.
Then for c we will let happen nothing.

So in the end of the strings if nothing is left in the STACK then we can say that language is accepted in the PDA.

---

We have designed the PDA for the problem:

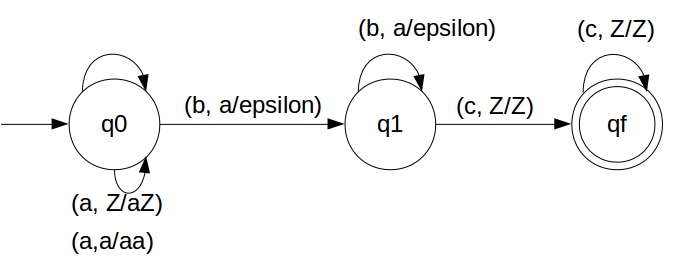
STACK Transiton Function

		δ(q0, a, Z) = (q0, aZ)            
		δ(q0, a, a) = (q0, aa)            
		δ(q0, b, a) = (q1, ε)     
		δ(q1, b, a) = (q1, ε)  

		             
		δ(q1, c, Z) = (qf, Z)

		δ(qf, c, Z) = (qf, Z)     

Note: qf is Final State

---

Explanation

Lets see, how this DPDA is working:
We will take one input string: "aabbcc"

1. Scan string from left to right
2. First input is 'a' and follow the rule:
3. on input 'a' and STACK alphabet Z, push the input 'a' into STACK as : (a,Z/aZ) and state will be q0
4. Second input is 'a' and so follow the rule:
5. on input 'a' and STACK alphabet 'a', push the input 'a' into STACK as : (a,a/aa) and state will be q0
6. Third input is 'b' and so follow the rule:
7. on input 'b' and STACK alphabet 'a', pop STACK with one 'a' as : (b,a/&epsiloon;) and state will be now q1
8. Fourth input is 'b' and so follow the rule:
9. on input 'b' and STACK alphabet 'a' and state is q1, pop STACK with one 'a' as : (b,a/&epsiloon;) and state will be q1
10. Fifth input is 'c' and top of STACK is Z so follow the rule:
11. on input 'c' and STACK alphabet 'Z' and state is q1, do nothing: (c,Z/Z) and state will be qf
12. Sixth input is 'c' and top of STACK is Z so follow the rule:
13. on input 'c' and STACK alphabet 'Z' and state is qf, do nothing: (c,Z/Z) and state will be qf
14. We reached end of the string, so follow the rule:
15. If we are standing at final state, qf then string is accepted in the PDA