Set Substitution Method to convert NFA to DFA

We convert NFA to DFA so that we can implement the state machine represented by DFA.
The method is as follows:

1. First find out the state transition table
2. Then take one state from the transtion table and then whenever you find out that output is not defined then put dead state there
3. Create new DFA

---

We will understand the whole menthod step by step:
Step 1:
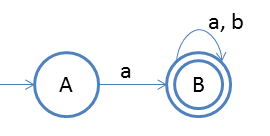
Following is the NFA for strings starting with 'a'

Step 2:
Create state transiton table

State	a	b
A	B	ϕ
B	B	B

Step 3:
Now create new transition table,
Rule is whenever there is ϕ, we will include one more state as dead state.

State	a	b
A	B	C
B	B	B
C	C	C

Note: Here C is a dead state
Step 4:
Now create new DFA from the new transition table

---

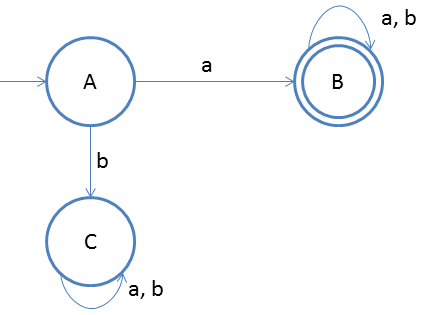
Note: Do not think that in the new table we will take the states which we have already, for example
If on state A for input 'a' we go to A and B both in NFA then we will write as

State	a	b
A	AB	D
AB	AB	B
D	D	D

---

If you did not get the point I have just mentioned then follow the below example, you will understand
Step 1:
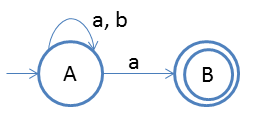
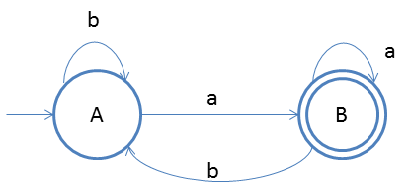
Following is the NFA for strings ending with 'a'

Step 2:
Create state transiton table

State	a	b
A	[AB]	A
B	ϕ	ϕ

Step 3:
Now create new transition table,
Rule is whenever there is ϕ, we will include one more state as dead state.

State	a	b
A	[AB]	[A]
[AB]	[AB]	[A]
D	D	D

Note: 1 Here State D goes to D on both inputs so we have not written it.
Note: 2 Here State [AB] is denoted by state B and [A] is denoted by state A.

Step 4:
Now create new DFA from the new transition table

Note: If there are n states in NFA then there could be 2ⁿ states in DFA after conversion.
Note: Final state(s) of DFA will be the one which includes final state of NFA

---

The proof of the above statement is explained by the below example:
Step 1:
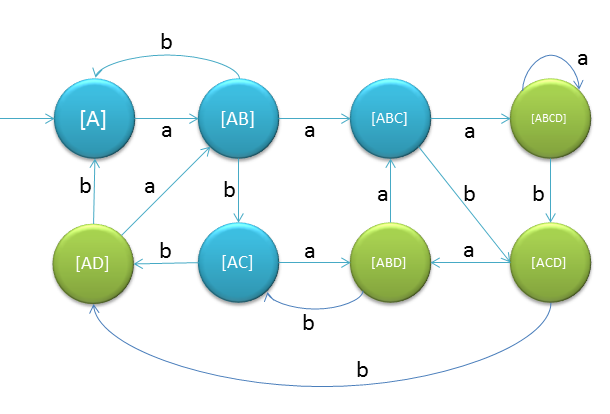
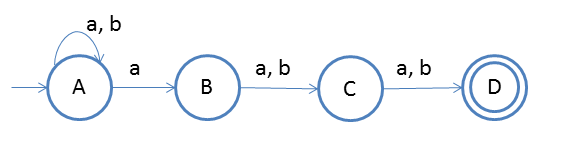
Following is the NFA for strings having 3^rd symbol 'a' from r.h.s.

Step 2:
Create state transiton table

State	a	b
A	{AB}	{A}
B	{C}	{C}
C	{D}	{D}
D*	ϕ	ϕ

Step 3:
Now create new transition table,
Rule is whenever there is ϕ, we will include one more state as dead state.

State	a	b
[A]	[AB]	[A]
[AB]	[ABC]	[AC]
[AC]	[ABD]	[AD]
[AD]	[AB]	[A]
[ABC]	[ABCD]	[ACD]
[ABD]	[ABC]	[AC]
[ACD]	[ABD]	[AD]
[ABCD]	[ABCD]	[ACD]

List of final states
[AD], [ABD], [ACD] and [ABCD] because they include D, final state of NFA.
Step 4:
Now create new DFA from the new transition table

---