DFA String Examples

Clearly the language is infinite because there is infinite number of strings.
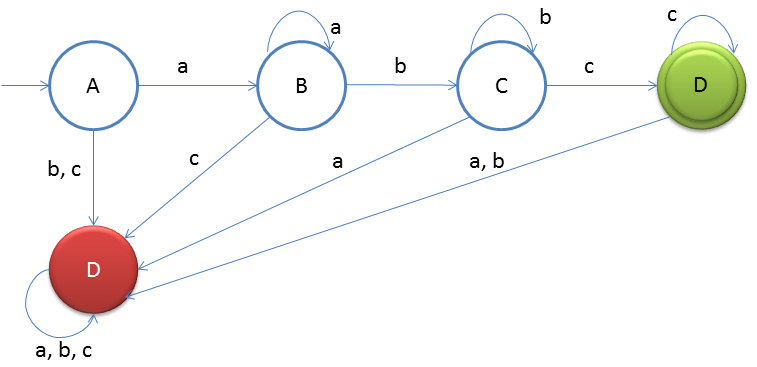The idea behind this approach is very simple, follow the steps below and you will understand.

1. Accept the smallest string 'abc' in the DFA that is four states will be made and state D will be made the final state
2. Now what if input 'b'/'c' comes on state A then it should be rejected as 'b'/'c' cannot come before 'a'
3. At state B if 'a' comes then we can loop it as no given DFA property will be violated
4. At state B if 'c' comes then it should be rejected as 'c' cannot come before 'b'
5. At state C if 'b' comes then we will loop it
6. At state C if 'a' comes then it should be rejected as 'a' cannot come after 'b'
7. At state C if 'c' comes then it should flow to state D
8. At state D if 'c' comes then we will loop it
9. At state D if 'a'/'b' comes then it should be rejected as 'a'/'b' cannot come after 'c'
10. State E will be Dead state and it will be looped for 'a', 'b' and 'c'

Testing

1. Lets take one input string aaabbbcc
2. Scan string from left to right
3. First input is a, so from state A we will go to state B
4. Second input is a, so from state B we will go to state B itself
5. Third input is a, so from state B we will go to state B itself
6. Fourth input is b, so from state B we will go to state C
7. Fifth input is b, so from state C we will go to state C itself
8. Sixth input is b, so from state C we will go to state C itself
9. Seventh input is c, so from state C we will go to state D
10. Eight input is c, so from state C we will go to state C itself(final state)