Introduction
Informally, a graph is a diagram consisting of points, called vertices, joined together by lines, called edges; each edge joins exactly two vertices. A graph G is a triple consisting of a vertex set of V(G), an edge set E(G), and a relation that associates with each edge two vertices (not necessarily distinct) called its endpoints.
Definition of Graph
A graph G = (V, E) consists of a (finite) set denoted by V, or by V(G) if one wishes to make clear which graph is under consideration, and a collection E, or E(G), of unordered pairs {u, v} of distinct elements from V. Each element of V is called a vertex or a point or a node, and each element of E is called an edge or a line or a link. Formally, a graph G is an ordered pair of dsjoint sets (V, E), where E Í V × V. Set V is called the vertex or node set, while set E is the edge set of graph G. Typically, it is assumed that self-loops (i.e. edges of the form (u, u), for some u Î V) are not contained in a graph.
Directed and Undirected Graph
A graph G = (V, E) is directed if the edge set is composed of ordered vertex (node) pairs. A graph is undirected if the edge set is composed of unordered vertex pair.Vertex Cardinality
The number of vertices, the cardinality of V, is called the order of graph and devoted by |V|. We usually use nto denote the order of G. The number of edges, the cardinality of E, is called the size of graph and denoted by |E|. We usually use m to denote the size of G.Neighbor Vertex and Neighborhood
We write vivj Î E(G) to mean {vi, vj}Î E(G), and if e = vi vj Î E(G), we say vi and vj are adjacent. Formally, given a graph G = (V, E), two vertices vi , vj Î V are said to be neighbors, or adjacent nodes, if ( vi , vj ) Î E. If G is directed, we distinguish between incoming neighbors of vi (those vertices vj Î V such that (vj, vi) Î E) and outgoing neighbors of vi (those vertices vj ÎV such that (vi, vj) Î E). The open neighborhood N(v) of the vertex v consists of the set vertices adjacent to v, that is, N(v) = {w Î v : vw Î E}. The closed neighborhood of v is N[v] = N(v) È {v}. For a set S Í V, the open neighborhood N(S) is defined to be UvÎSN(v), and the closed neighborhood of S is N[S] = N(S) È S.Vertex Degree
The degree deg(v) of vertex v is the number of edges incident on v or equivalently, deg(v) = |N(v)|. The degree sequence of graph is (deg(v1), deg(v2), ..., deg(vn)), typically written in nondecreasing or nonincreasing order. The minimum and maximum degree of vertices in V(G) are denoted by d(G) and ∆(G), respectively. If d(G) = ∆(G) = r, then graph G is said to be regular of degree r, or simply r-regular.
Formally, given a graph G = (V, E), the degree of a vertex v Î V is the number of its neighbors in the graph. That is,
deg(v) = | {u Î V : (v, w) Î E}|.
If G is directed, we distinguish between in-degree (nimber of
incoming neighbors) and out-degree (number of outgoing neighbors) of a vertex.
Loop and Multiple Edges
A loop is an edge whose endpoints are equal i.e., an edge joining a vertex to it self is called a loop. We say that the graph has multiple edges if in the graph two or more edges joining the same pair of vertices.
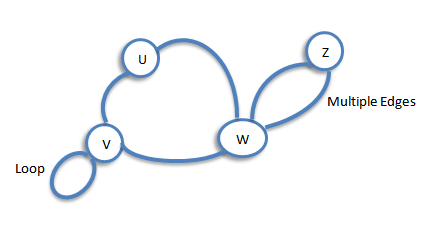
Simple Graph
A graph with no loops or multiple edges is called a simple graph. Wespecify a simple graph by its set of vertices and set of edges, treating the edge set as a set of unordered pairs of vertices and write e = uv (or e = vu) for an edge e with endpoints u and v.

When u and v are endpoints of an edge, they are adjacent and are neighbors.
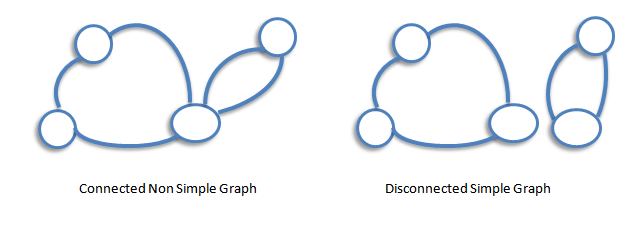
Connected Graph
A graph that is in one piece is said to be connected, whereas one which splits into several pieces is disconnected.
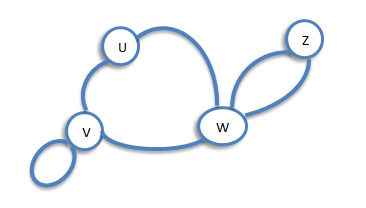
Subgraph
Let G be a graph with vertex set V(G) and edge-list E(G). A subgraph of G is a graph all of whose vertices belong to V(G) and all of whose edges belong to E(G). For example, if G is the connected graph below:
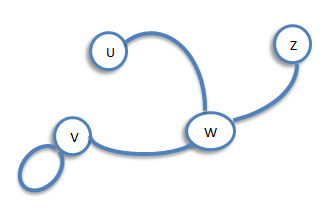
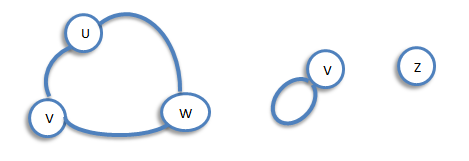
Degree (or Valency)
Let G be a graph with loops, and let v be a vertex of G. The degree of v is the number of edges meeting at v, and is denoted by deg(v). For example, consider, the following graph G
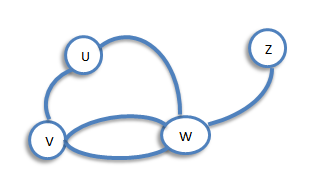
Regular Graph
A graph is regular if all the vertices of G have the same degree. In particular, if the degree of each vertex is r, the G is regular of degree r.
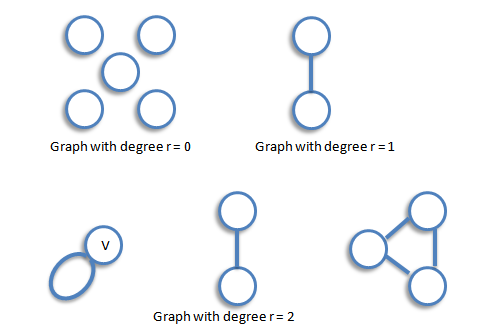
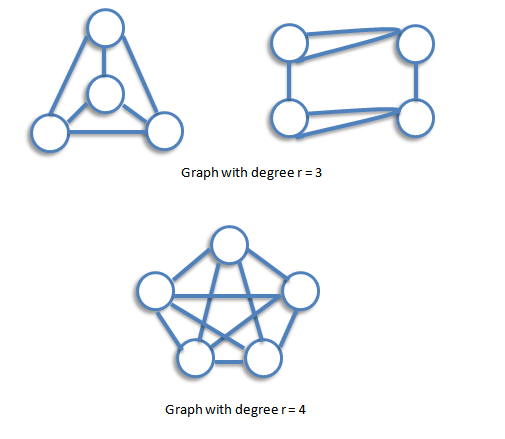
The Handshaking Lemma
In any graph, the sum of all the vertex-degree is equal to twice the number of edges.
Proof
Since each edge has two ends, it must contribute exactly 2 to the sum of the degrees. The result follows immediately.
The Following are the consequences of the Handshaking lemma.=
- In any graph, the sum of all the vertex-degree is an even number.
- In any graph, the number of vertices of odd degree is even.
- If G is a graph which has n vertices and is regular of degree r, then G has exactly 1/2 nr edges.
Isomorphic Graphs
Two graph G and H are isomorphic if H can be obtained from G by relabeling the vertices - that is, if there is a one-to-one correspondence between the vertices of G and those of H, such that the number of edges joining any pair of vertices in G is equal to the number of edges joining the corresponding pair of vertices in H. For example, two unlabeled graphs, such as
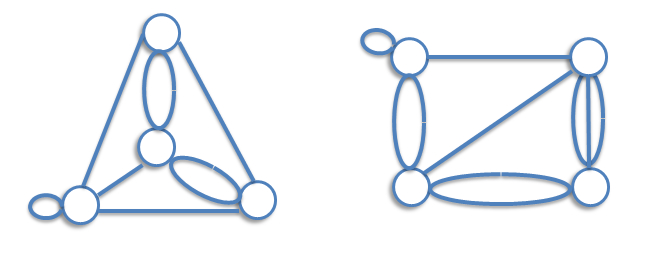
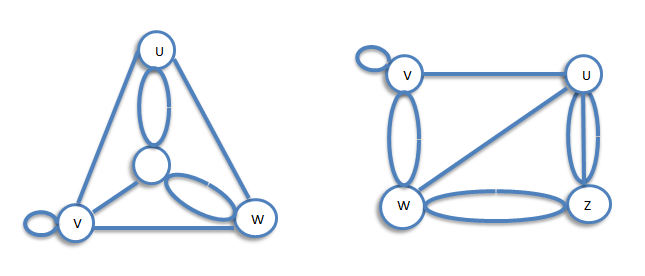
Complete Graphs
A computer graph is a graph in which every two distinct vertices are joined by exactly one edge. The complete graph with n vertices is denoted by Kn. The following are the examples of complete graphs.
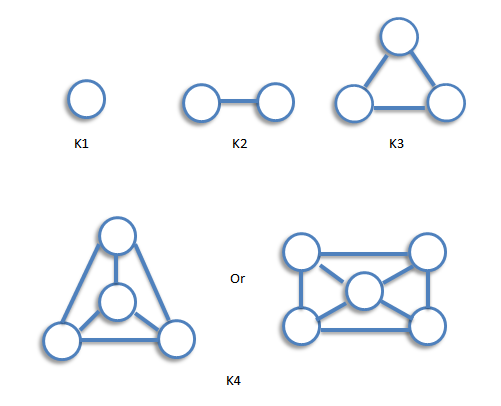
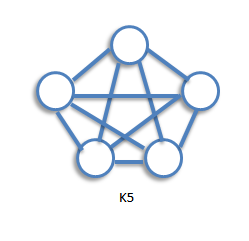
The graph Kn is regular of degree n-1, and therefore has 1/2n(n-1) edges, by consequence 3 of the handshaking lemma.
