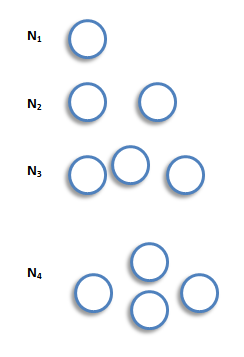
Null Graphs

A null graphs is a graph containing no edges. The null graph with n vertices is denoted by N_n. The following are the examples of null graphs.

 

Note that N_n is regular of degree 0.

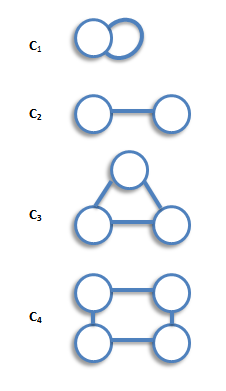
Cycle Graphs

A cycle graph is a graph consisting of a single cycle. The cycle graph with n vertices is denoted by C_n. The following are the examples of cyclic graphs.

 

Note that  C_n is regular of degree 2, and has n edges.

 

Path Graphs

A path graph is a graph consisting of a single path. The path graph with n vertices is denoted by P_n. The following are the examples of path graphs.

 

 

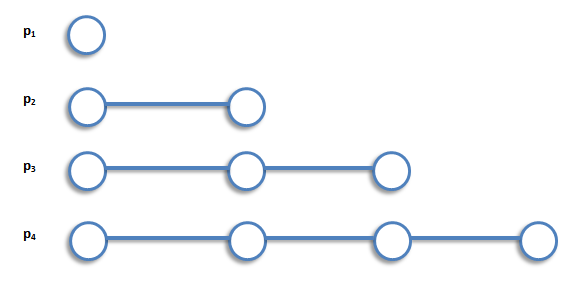
Note that path graph, P_n, has n-1 edges, and can be obtained from cycle graph, C_n, by removing any edge.

 

 

Bipartite Graphs

A bipartite graph is a graph whose vertex-set can be split into two sets in such a way that each edge of the graph joins a vertex in first set to a vertex in second set. The examples of bipartite graphs are:

6.25 4.36 9.02 3.68

 

 

 

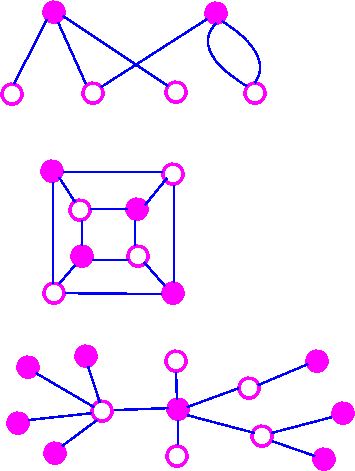
Complete Bipartite Graph

A complete bipartite graph is a bipartite graph in which each vertex in the first set is joined to each vertex in the second set  by exactly one edge. The complete bipartite graph with r vertices and 3 vertices is denoted by K_r,s. The following are some examples.

 

 

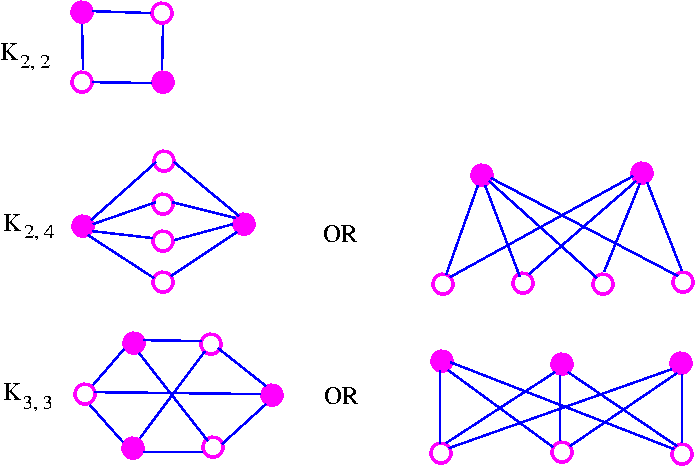
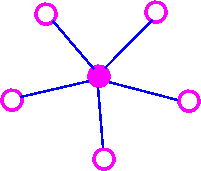
Note that K_r,s has r+s vertices (r vertices of degrees, and s vertices of degree r), and rs edges. Note also that  K_r,s = K_s,r. An Important Note:    A complete bipartite graph of the form K_r,s is called a star graph.

 

Cube Graph

The cube graphs is a bipartite graphs and have appropriate in the coding theory. The cube graphs constructed by taking as vertices all binary words of a given length and joining two of these vertices if the corresponding binary words differ in just one place. The binary words of length k is called the k-cube (or k-dimensional cube) graph and is denoted by Q_k. The following are some examples.

 

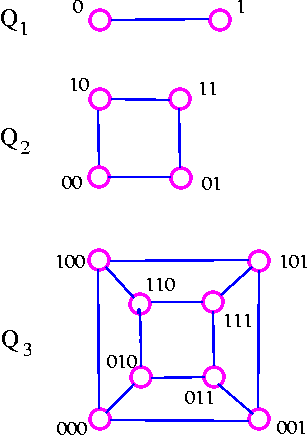
Note that Q_k has 2^k vertices and is regular of degree k. It follows from consequence 3 of the handshaking lemma that Q_k has k* 2^k-1 edges.

 

 

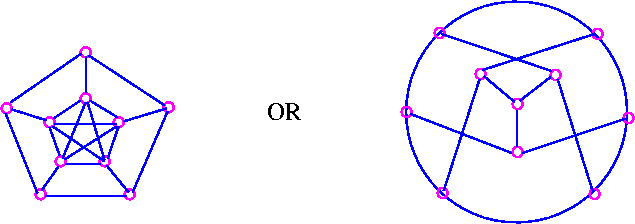
The Peterson Graph

This graph is named after a Danish mathematician, Julius Peterson(1839-1910), who discovered the graph in a paper of 1898.

 

 

Tree Graph

A tree is a connected graph which has no cycles.

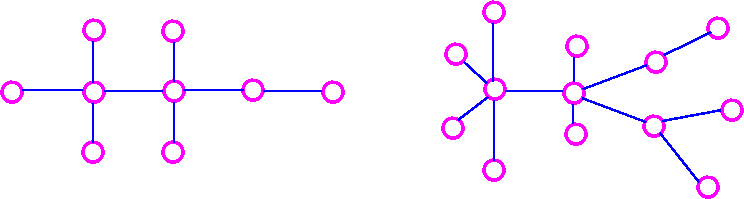
Spanning Tree

If G is a connected graph, the spanning tree in G is a subgraph of G which includes every vertex of G and  is also a tree. Consider the following graph

The following are the three of its spanning trees:

Interval Graphs

Consider the intervals (0, 3), (2, 7), (-1, 1), (2, 3), (1, 4), (6, 8) which may be illustrated as

We can construct the resulting interval graphs by taking the interval as vertices, join two of these vertices by an edge whenever the corresponding intervals have at least one point in common.

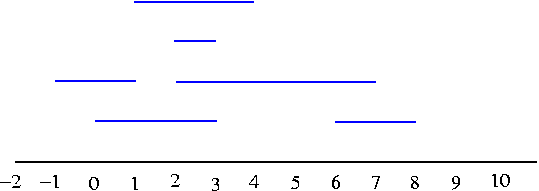
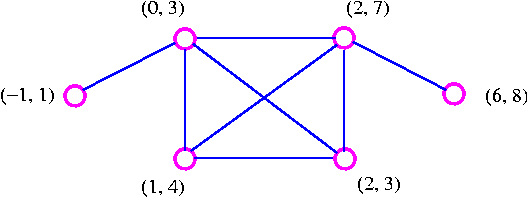
Note that since the intervals (-1, 1) and (1, 4) are open intervals, they do not have a point in common.

 

 

Definition of Diagraph

A directed graph or diagraph D consists of a set of elements, called vertices, and a list of ordered pairs of these elements, called arcs. The set of vertices is called arcs. The set of vertices is called the vertex-set of D, denoted by V(D), and the list of arcs is called the arc-list of D, denoted by A(D). If v and w are vertices of D, then an arc of the form vw is said to be directed from v to w, or to join v to w.

 

 

 

 The underlying graph of diagraph is the graph obtained by replacing each arc of diagraph by corresponding (undirected) edge. For example, consider the following digraph

The underlying graph of the above digraph is