Cross Product Method over DFAs

We will try to understand this property using one example.

---

---

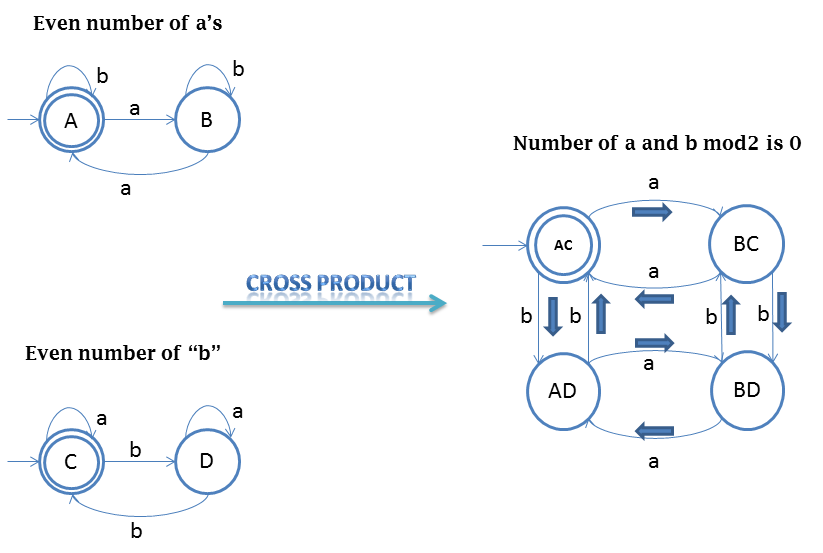
So as you see in the above picture, we have taken two DFAs

1. Even no of a's
2. Even no of b's

Languages represented by them are respectively

1. L1 = {ε, baa, aa, aba, aab, aaaa, ... }
2. L2 = {ε bb, abb, bab, bba, ...}

---

After taking cross product we will find the below DFA, already we have seen this DFA in previous exampels
As, L = {ab, aab, abb, aaab, ...}

---

How we have designed:

{A, B} X {C, D} = {AC, AD, BC, BD}
We should know the transition of the above four states

Note: clearly the language is infinite
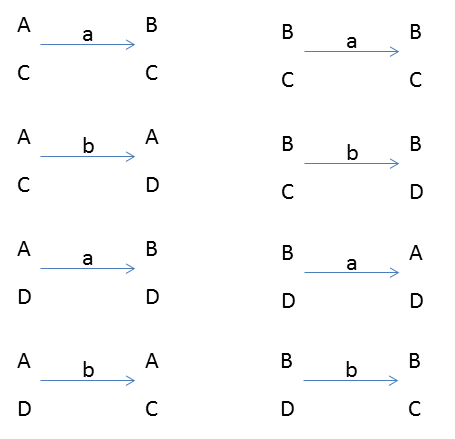
You can also take some examples from the previous exercises for practice.

---