DFA

DFA or deterministic finite automata has one output for one input alphabet from a state.

Classification of Finite Automata

We will explain DFA for now, rest of them we will talk about later.
Below are symbols used in the DFA:

1. Q - Finite set of states
2. Σ - Input alphabet
3. δ - QxΣ → Q
4. q0 - start state
5. F - Final State

Note: Q ⊇ F

---

Question 1

Construct a DFA which accepts set of all strings over Σ={a,b} of length 2 , L = {aa, ab, ba, bb}
Ans

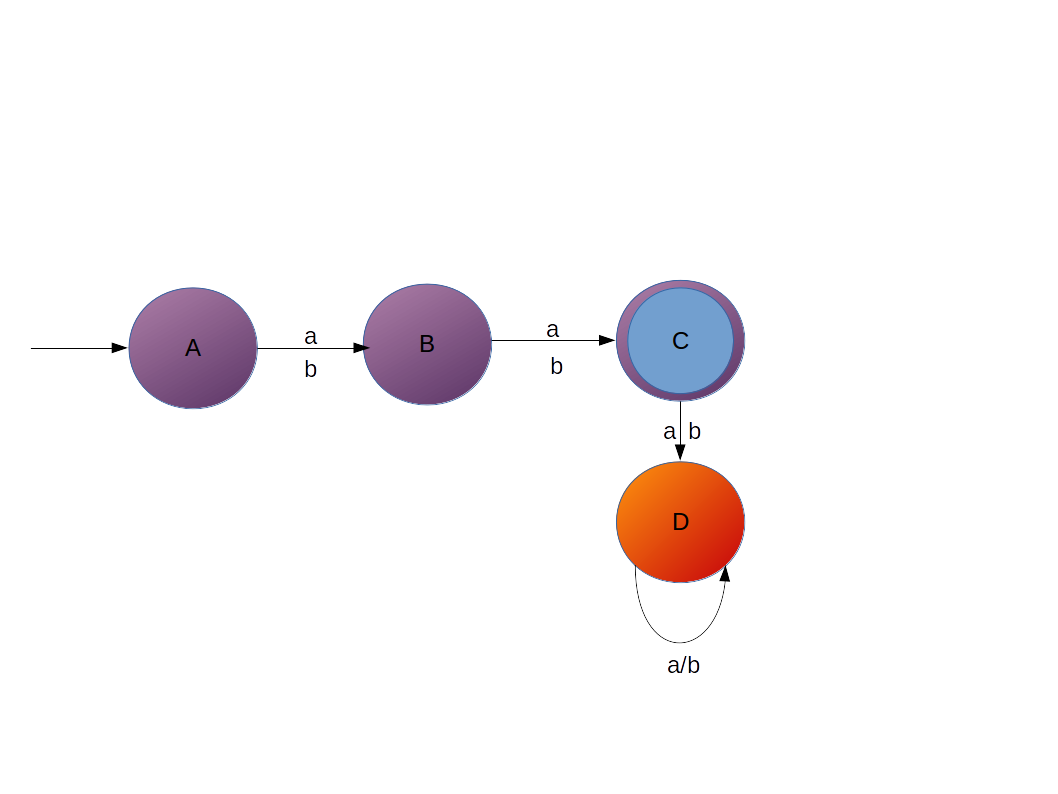
Explanation

1. We have to create DFA which will accept string of length 2 on alphabet {a, b}
2. So first thing about creating DFA which will accept of 1 length string, that is pretty simple
3. You just take 2 states 1 length string can be accepted. Now take 2 length stirng for that we need 3 states
4. And third state will be final state.
5. But what if we came up with a string of length 3, it should not be accepted in our DFA, right ?
6. So we have to attach one more state to take care of string greater than 2.
7. State 'D' is called dead state.

---

Languages Acceptance

When we say language is accepted in DFA then all the strings belonging to language should be accepted
in the DFA and the strings which are not part of the language should not be accepted in the DFA.

---

Question 2 Construct a DFA which accepts set of all strings over Σ={a,b} of length ≥2

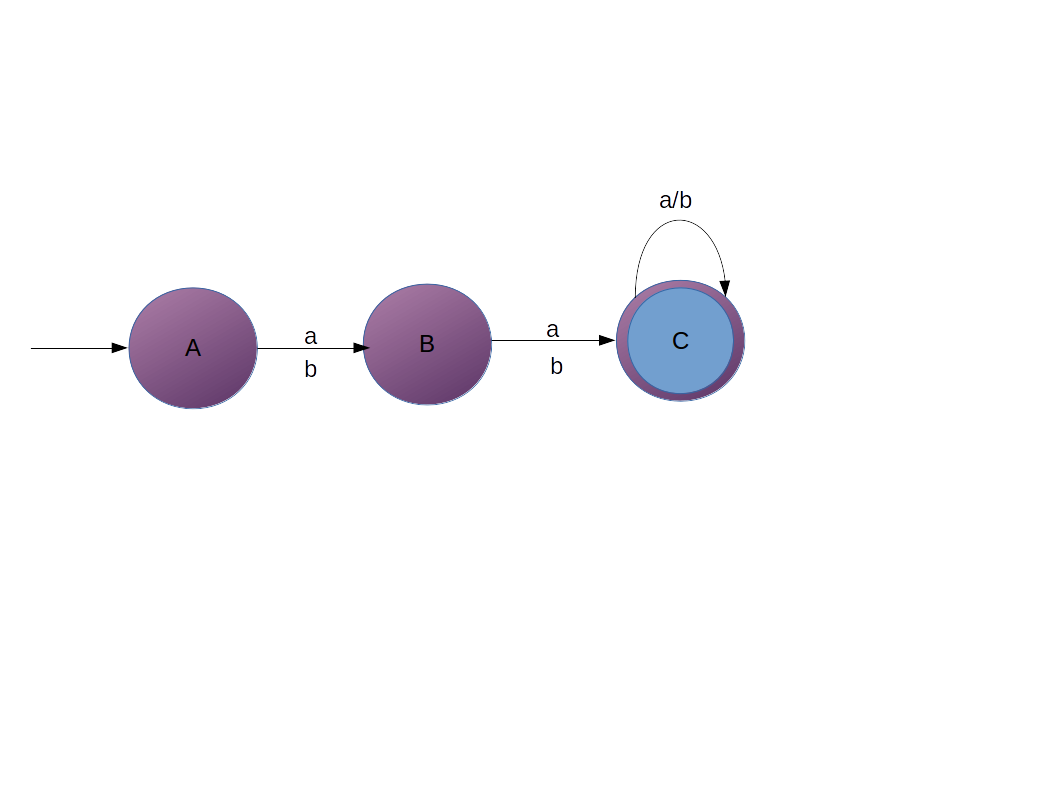
Explanation
We have to create DFA which will accept string of length ≥ 2 on alphabet {a, b}.

1. So again first thing about creating DFA which will accept of 1 length string, that is pretty simple.
2. You just take 2 states 1 length string can be accepted.
3. Now take 2 length stirng for that we need 3 states.
4. And third state will be final state.
5. And if input comes over state C then it will go to C itself to accept strings greater than 2
6. Now if string < 2 will not reach final state, so will not be accepted.

Testing

1. Suppose we have abab, so take alphabets from left to right
2. firstly 'a' came on start state A, then we will go to state B
3. then input came as 'b', so on state B we will go to state C.
4. then 'a', we go to C itself
5. then 'b', we go to C itself
6. At the end of the string we are at final state, so we say that string is accepted
7. And for the strings which are less than 2, you will not reach final state.

---

Question 3 Construct a DFA which accepts set of all strings over Σ={a,b} of length ≤2

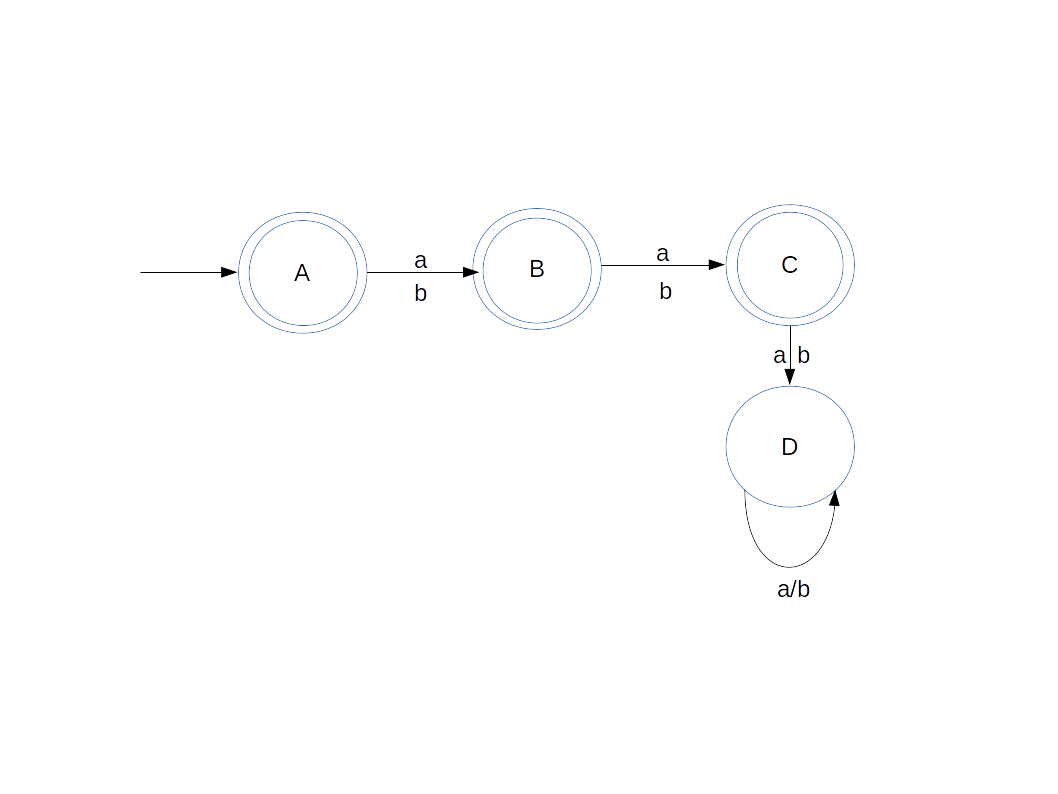
Explanation
We have to create DFA which will accept string of length ≤ 2 on alphabet {a, b}.

1. Think about the language content = {∈,a, b, ab, ba, bb, aa}
2. So again first thing about creating DFA which will accept of ∈, that is first state will be final state
3. Then we have to accept single letter that is two states will be required and second state also will be final state
4. Now we need to accept 2 input symbols one after another in case of aa or ab or bb or ba
5. And strings which are greater than 3 should not be accepted.
6. So we have to attach 1 more state as dead state.

Testing Example 1

1. Suppose we have ∈ (empty string), so take alphabets from left to right
2. It will accepted as first state is final state and that means on nothing you are at final state.

Testing Example 2

1. Suppose string is ab
2. firstly 'a' came on start state A, then we will go to state B
3. then input came as 'b', so on state B we will go to state C.
4. At the end of the string we are at final state C, so we say that string is accepted

And for the strings which are less than 2, you will not reach final state.

So in general we can say that:

n+2

Length of String	No of states
|w|=n	n+2
|w|≥n	n+1
|w|≤n

Example 4

Create a DFA which accepts strings of even length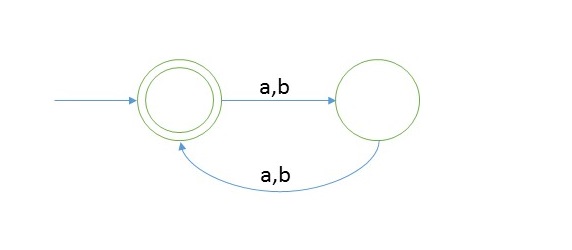

Explanation
As we can see that length of string should be even for that language will be = {Σab, aa, bb, ba, aaaa, bbbb, ….}
And the language is infinite.

Testing

1. Take a string ‘abbb’ to test whether it is accepted in the above DFA
2. Scan string from left to right
3. first input we get is a and from start state on ‘a’ we go to the second state
5. second input is b, from second state on b we will go to start state again.
6. third input is b, from start state we go to second state.
7. from second state we go to first state on fourth input symbol.
8. Now we reached end of string and we are standing on final state.

So we say that string is accepted.

---

Examples

1. DFA which accepts strings of odd length
2. Design a DFA over w ∈ {a,b}^* such that number of a = 2 and there is no restriction over length of b
3. DFA for Number of a(w) mod 2 = 0 and Number of b(w) mod 2 = 0
4. DFA for Number of a(w) mod 2 = 0 or Number of b(w) mod 2 = 0
5. DFA for Number of a(w) mod 2 != 0 and Number of b(w) mod 2 != 0
6. DFA for Number of a(w) mod 3= 0 and Number of b(w) mod 3= 0
7. DFA for Number of a(w) mod 3 > Number of b(w) mod 3
8. DFA for binary number divisible by 2
9. DFA for binary number divisible by 3
10. DFA in which set of all strings can be accepted which start with a
11. DFA in which set of all strings can be accepted which contains ‘a’
12. DFA in which set of all strings can be accepted which end with ‘a’
13. DFA in which set of all strings can be accepted which start with ab
14. DFA in which set of all strings can be accepted which contain ab
15. DFA in which set of all strings can be accepted which ends with ab
16. DFA in which start and end symbol must be different
17. Design a DFA in which start and end symbol must be same
18. DFA in which every 'a' should be followed by 'b'
19. DFA in which every 'a' should never followed by 'b'
20. DFA in which every 'a' should followed by 'bb'
21. DFA in which every 'a' should never followed by 'bb'
22. DFA for aⁿb^m | n,m ≥ 1
23. DFA for aⁿb^m | n,m ≥ 0
24. DFA for aⁿb^mc^l | n,m,l ≥ 1
25. DFA for aⁿb^mc^l | n,m,l ≥ 0
26. DFA such that second sybmol from L.H.S. should be 'a'

---