DFA String Examples

Clearly the language is infinite because there is infinite number of strings.
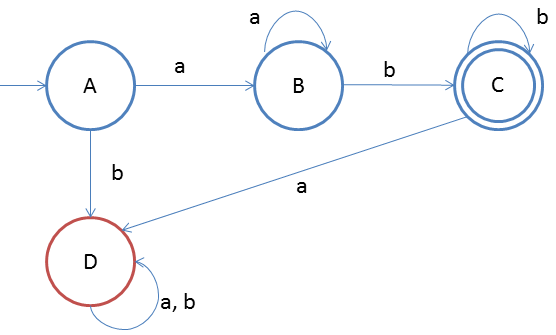The idea behind this approach is very simple, follow the steps below and you will understand.

1. Firstly make DFA for smallest string that is ab, so three states will A, B and C, C being final state
2. Now 'a' come multiple times so we have to loop on state B. Cause 'a' will always come before 'b'
3. At state C if b comes then we have to loop it
4. If 'b' comes on state A then we have to reject it, direct the flow to state D(dead state)
5. If 'a' comes on state C then we have to reject it, direct the flow to state D(dead state)

Testing

1. Lets take one input string aaabbbb
2. Scan string from left to right
3. First input is a, so from state A we will go to state B
4. Second input is a, so from state B we will go to state B itself
5. Third input is a, so from state B we will go to state B itself
6. Fourth input is b, so from state B we will go to state C(final state)
7. Fifth input is b, so from state B we will go to state C(final state)
8. Sixth input is b, so from state B we will go to state C(final state)
9. Seventh input is b, so from state B we will go to state C(final state)