DPDA for number of a(w) = number of b(w)

Here approach is little bit different than previous example.

Let either 'a' or 'b' push in STACK. That means if 'a' comes first let it push.
After 'a' if again 'a' comes then let push it.

If 'b' comes first, push it in STACK ('a' did not come yet)
If again 'b' comes then push it in STACK.

Now if 'a' is present in top of STACK and 'b' comes then, pop 'a'
Similarily if 'b' is present in top of STACK and 'a' comes then, pop 'b'

So in the end of the strings if nothing is left in the STACK then we can say that CFL is accepted in the PDA.

---

We have designed the PDA for the problem:

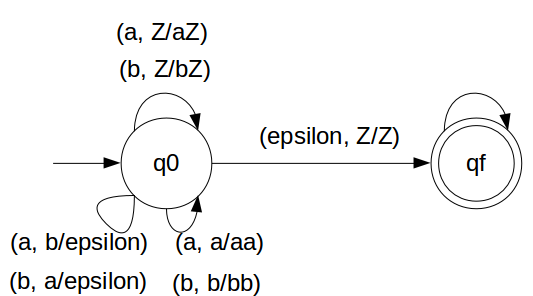
STACK Transiton Function

		δ(q0, a, Z) = (q0, aZ)     
		δ(q0, a, a) = (q0, aa)     
		δ(q0, b, Z) = (q0, bZ)     
		δ(q0, b, b) = (q0, bb)     
		δ(q0, b, a) = (q0, ε)     
		δ(q0, a, b) = (q0, ε)     

		δ(q0, ε, Z) = (qf, Z)     

Note: qf is Final State

---

Explanation

Lets see, how this DPDA is working:
We will take one input string: "aabbbbaa"

1. Scan string from left to right
2. First input is 'a' and follow the rule:
3. on input 'a' and STACK alphabet Z, push the input 'a' into STACK as : (a,Z/aZ) and state will be q0
4. Second input is 'a' and so follow the rule:
5. on input 'a' and STACK alphabet 'a', push the input 'a' into STACK as : (a,a/aa) and state will remain q0
6. Second input is 'b' and so follow the rule:
7. Third input is 'b' and so follow the rule:
8. on input 'b' and STACK alphabet 'a', pop STACK with one 'a' as : (b,a/&epsiloon;) and state will remain q0
9. Fourth input is 'b' and so follow the rule:
10. on input 'b' and STACK alphabet 'a', pop STACK with one 'a' as : (b,a/&epsiloon;) and state will remain q0
11. Fifth input is 'b' and so follow the rule:
12. on input 'b' and STACK alphabet Z, push the input 'b' into STACK as : (b,Z/bZ) and state will remain q0
13. Sixth input is 'b' and so follow the rule:
14. on input 'b' and STACK alphabet 'a', push the input 'b' into STACK as : (b,b/bb) and state will remain q0
15. Seventh input is 'a' and so follow the rule:
16. on input 'a' and STACK alphabet 'b', pop STACK with one 'b' as : (a,b/&epsiloon;) and state will remain q0
17. Eighth input is 'a' and so follow the rule:
18. on input 'a' and STACK alphabet 'b', pop STACK with one 'b' as : (a,b/&epsiloon;) and state will remain q0
19. We reached end of the string, so follow the rule:
20. on input ε and STACK alphabet Z, go to final state(qf) as : (ε, Z/Z)