Recursive Enumerable Language
For a given language if a turing machine can be designed then that language will be recursive enumerable language.
Halting Problem
If turing machine answers YES for string belonging to language.But for string not belonging to language Turing Machine can either answer NO or it could go into infinite loop.
Then this is called Halting problem and such a language is called Recursie Enumerable Language.
Below picture will put more light on the explanation:
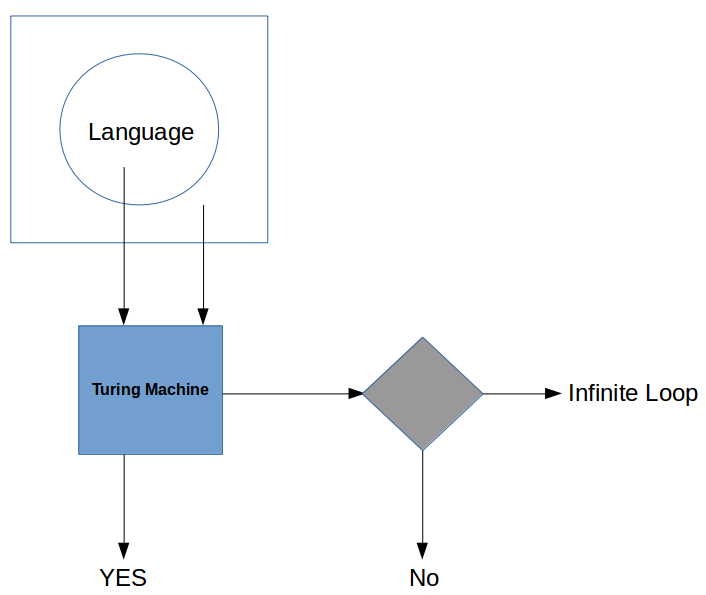
In above pic the outer rectangle is Σ*(all possible strings over given input) and langauge is a subset of it.
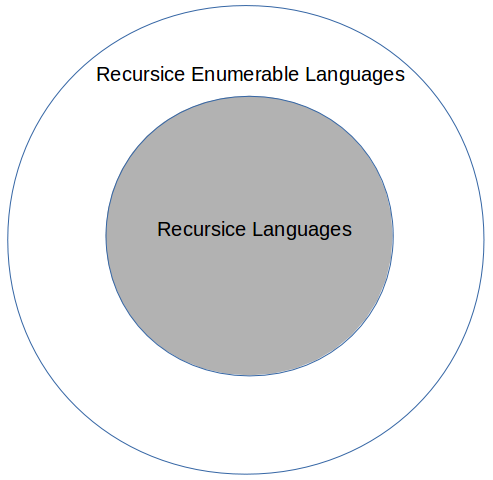
Recursive Enumerable and Recursive Langauges
Recursive Enumerable languages are superset of Recursive Langauges.Means: Every recusrive language is recursive enumerable language but vice-versa is not true.
Recursive Enumerable Langauge Closure Properties
| Closure Property | Status |
|---|---|
| Union | Yes |
| Intersection | Yes |
| Set Difference | No |
| Compliment | No |
| Intersection with Regular Language | Yes |
| Concatination | Yes |
| Kleen Closure | Yes |
| Kleen Plus | Yes |
| Reversal | Yes |
| Homomorphism | Yes |
| ε-free Homomorphismx | Yes |
| Inverse Homomorphism | Yes |
| Substitution | Yes |
| ε-free Substitution | Yes |
