NPDA for ww^R w ε (a,b)^*

In this example we will discuss NPDA
NPDA are designed when there is no subtle decision like we did in previous example on arrival of 'c'
So now we have to design a machine which can bruteforce the answer.
We have designed the PDA for the problem:

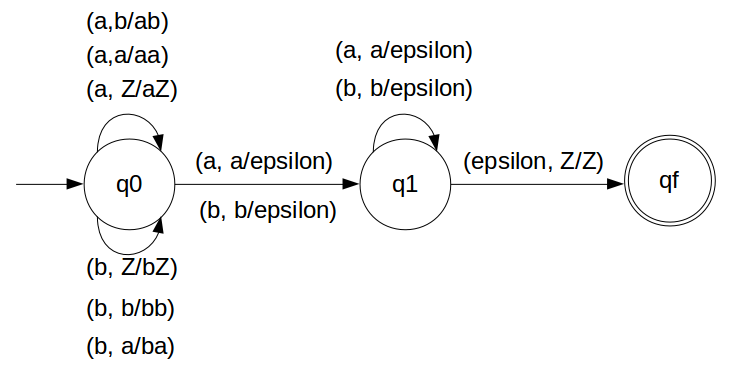
STACK Transiton Function

		δ(q0, a, Z) = (q0, aZ)            
		δ(q0, a, a) = (q0, aa)            
		δ(q0, b, Z) = (q0, bZ)            
		δ(q0, b, b) = (q0, bb)
		δ(q0, a, b) = (q0, ab)            
		δ(q0, b, a) = (q0, ba)            
			
		// this is decision step	
		δ(q0, a, a) = (q1, ε)
		δ(q0, b, b) = (q1, ε)

		δ(q1, b, b) = (q1, ε)     
		δ(q1, a, a) = (q1, ε)     

		δ(q1, ε, Z) = (qf, Z)     

Note: qf is Final State

---

Explanation

Lets see, how this DPDA is working:
We will take one input string: "abbbba"

Scan string from left to right

First input is 'a' and follow the rule:

on input 'a' and STACK alphabet Z, push the two 'a's into STACK as : (a,Z/aZ) and state will be q0

Second input is 'b' and so follow the rule:

on input 'b' and STACK alphabet 'a', push the 'b' into STACK as : (b,a/ba) and state will be q0

Third input is 'b' and so follow the rule:

on input 'b' and STACK alphabet 'b', push the 'b' into STACK as : (b,b/bb) and state will be q0

Here we will assume that one delimeter comes either that could be 'a' or 'b'

Forth input is 'b' and so follow the rule:

on input 'b' and STACK alphabet 'b' (state is q1), pop one 'b' from STACK as : (b,b/ε) and state will be q1

Fifth input is 'b' and so follow the rule:

on input 'b' and STACK alphabet 'b' (state is q1), pop one 'b' from STACK as : (b,b/ε) and state will be q1

Sixth input is 'a' and so follow the rule:

on input 'a' and STACK alphabet 'a' and state q1, pop one 'a' from STACK as : (a,a/ε) and state will remain q1

We reached end of the string, so follow the rule:

on input ε and STACK alphabet Z, go to final state(qf) as : (ε, Z/Z)

---

Here a decision tree will get formed to come to the solution.

---

Thus NPDA is more powerful than DPDA