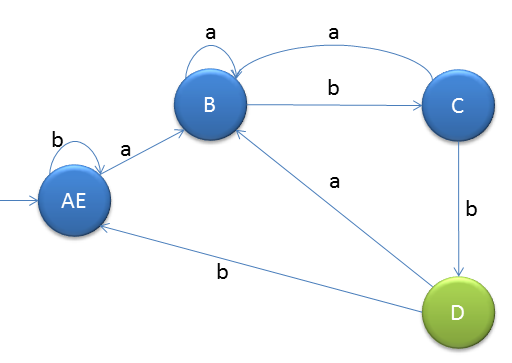
Minimisation of DFA

We will minimise DFA using partition method.We will get unique DFA after minimisation.

---

First understand that when two states will be equivalent
δ(p,w) ε F => δ(q,w) ε F
δ(p,w) ∉ F => δ(q,w) ∉ F

If p and q are equivalent then we can combine them into 1.

---

Follow the steps:

1. Identify start and final state.
2. Create transition table
3. Delete the states which are not accessible from initial state
4. Then find the n^th equivalent sets for n=0 till the sets are not changing
5. Create new DFA

---

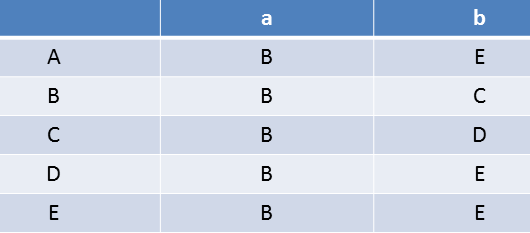
Now make transition table

Here "D" is final state and "A" is start state

---

We will start the method by finding

0 equivalent

That is divide two sets, one is final states and another is non-final states
So we will get below two set of states
[A,B,C,E] and [D]

---

1 equivalent

Now try to divide the sets into subsets by comparing two states' output on some symbol
If the output states are in the same sets then the two states will remain in same set otherwise split them in subsets.
If you are not getting then just go through this example completly and you will understand

---

Now we will find the 1 equivalent
[A,B,C,E] and [D], from here compare A and B with their output states,
Check for A and B
As we see A's output on 'a' is B and B's output on 'a' is also B. And A's output on 'b' is E and B's output on 'b' is C. Both E and C are in same set in 0 equivalent so states A and B remain in same set.

Check for A and C
As we see A's output on 'a' is B and C's output on 'a' is also B. And A's output on 'b' is E and C's output on 'b' is D. Both E and C are not in same set in 0 equivalent so states A and C will not remain in same set.
So we will create one more subset conaining state C

As, [A,B,E], [C] and [D]

---

2 equivalent

[A,B,E], [C] and [D]
So find out for A and B : A's o/p on 'a' is B and B's o/p on 'a' is B, so no issues. But check for second input 'b'.
A's o/p on 'b' is E and B's o/p on 'b' is C which are in different sets, so we split.

[A,E], [B], [C] and [D]

3 equivalent

Check for A and E, but if you see o/p of A and E are in the same set.
[A,B,E], [C] and [D]
So we stop here as there is no change.
Note:Also try to combine the splited sets if possible, means try to combine B and C, but they have o/p(s) in different sets so cannot combine them

---

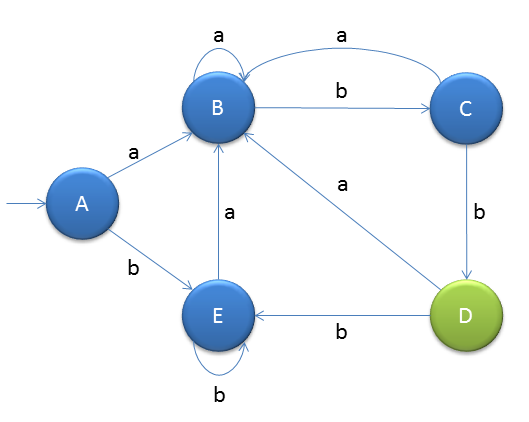
Create new DFA with the 3 equivalent sets

---