Dijkstra's Algorithm

Dijkstra's algorithm is a greedy algorithm that solves the shortest path problem for a directed graph G.
Dijkstra's algorithm solves the single-source shortest-path problem when all edges have non-negative weights.

---

Dijkstra's Algorithm

DIJKSTRA(G,s)
1 INITIALIZE-SINGLE-SOURCE(G, S)
2 S ← Ø
3 Q ← V[G]
4 while Q ≠ Ø
5 	do u ← EXTRACT-MIN(Q)
6 		S ← S U {u}
7 			for each vertex v ∈ Adj[u]
8				do if dist[v] > dist[u] + w(u,v)
9     				  then d[v] ←d[u] + w(u,v) 

INITIALIZE-SINGLE-SOURCE( Graph g, Node s )
   dist[s] = 0;
   for each vertex v in Vertices V[G] - s
       dist[v] ← ∞

---

Example

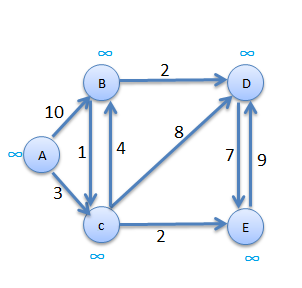
Procedure for Dijkstra's Algorithm

Step1

Consider A as source vertex

No. of Nodes        A        B        C        D        E Distance        0        10        3        ∞        ∞ Distance From               A        A

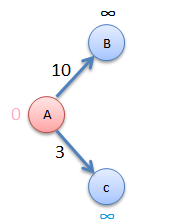
Step2

Now consider vertex C

No. of Nodes        A        B        C        D        E Distance        0        7        3        11        5 Distance From               C        C        C        C

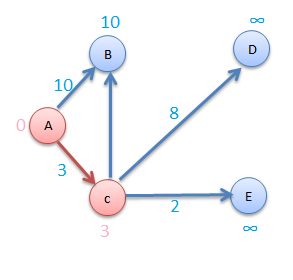
Step3

Now consider vertex E

No. of Nodes        A        B        C        D        E Distance        0        7        3        11        0 Distance From               C        A        C        E

Step4

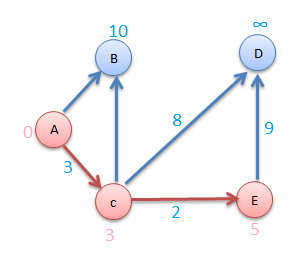
Now consider vertex B

No. of Nodes        A        B        C        D        E Distance        0        7        3        9        5 Distance From               C        A        B        C

Step5

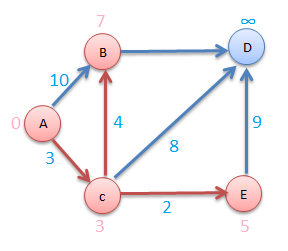
Now consider vertex D

No. of Nodes        A       B        C        D        E Distance        0        7        3        9        11 Distance From        A        C        A        B        C

---

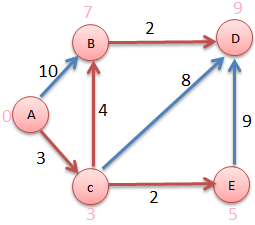
	A	B	C	D	E
	0	∞	∞	∞	∞
A	0	10	3	∞	∞
C		7	3	11	5
E				14	5
B				9
D					16

---

C FUNCTION of Dijkstra's Algorithm

void dijikstra(int G[MAX][MAX], int n, int startnode)
{
	int cost[MAX][MAX], distance[MAX], pred[MAX];
	int visited[MAX], count, mindistance, nextnode, i,j;
	for(i=0;i < n;i++)
		for(j=0;j < n;j++)
			if(G[i][j]==0)
				cost[i][j]=INFINITY;
			else
				cost[i][j]=G[i][j];
	
	for(i=0;i< n;i++)
	{
		distance[i]=cost[startnode][i];
		pred[i]=startnode;
		visited[i]=0;
	}
	distance[startnode]=0;
	visited[startnode]=1;
	count=1;
	while(count < n-1){
		mindistance=INFINITY;
		for(i=0;i < n;i++)
			if(distance[i] < mindistance&&!visited[i])
			{
				mindistance=distance[i];
				nextnode=i;
			}
		visited[nextnode]=1;
		for(i=0;i < n;i++)
			if(!visited[i])
				if(mindistance+cost[nextnode][i] < distance[i])
				{
					distance[i]=mindistance+cost[nextnode][i];
					pred[i]=nextnode;
				}
			count++;
	}

	for(i=0;i < n;i++)
		if(i!=startnode)
		{
			printf("\nDistance of %d = %d", i, distance[i]);
			printf("\nPath = %d", i);
			j=i;
			do
			{
				j=pred[j];
				printf(" <-%d", j);
			}
			while(j!=startnode);
		}
}

---

C IMPLEMETATION of Dijkstra's Algorithm

#include<stdio.h>
#include<conio.h>
#define INFINITY 9999
#define MAX 10

void dijikstra(int G[MAX][MAX], int n, int startnode);

void main(){
	int G[MAX][MAX], i, j, n, u;
	clrscr();
	printf("\nEnter the no. of vertices:: ");
	scanf("%d", &n);
	printf("\nEnter the adjacency matrix::\n");
	for(i=0;i < n;i++)
		for(j=0;j < n;j++)
			scanf("%d", &G[i][j]);
	printf("\nEnter the starting node:: ");
	scanf("%d", &u);
	dijikstra(G,n,u);
	getch();
}

void dijikstra(int G[MAX][MAX], int n, int startnode)
{
	int cost[MAX][MAX], distance[MAX], pred[MAX];
	int visited[MAX], count, mindistance, nextnode, i,j;
	for(i=0;i < n;i++)
		for(j=0;j < n;j++)
			if(G[i][j]==0)
				cost[i][j]=INFINITY;
			else
				cost[i][j]=G[i][j];
	
	for(i=0;i< n;i++)
	{
		distance[i]=cost[startnode][i];
		pred[i]=startnode;
		visited[i]=0;
	}
	distance[startnode]=0;
	visited[startnode]=1;
	count=1;
	while(count < n-1){
		mindistance=INFINITY;
		for(i=0;i < n;i++)
			if(distance[i] < mindistance&&!visited[i])
			{
				mindistance=distance[i];
				nextnode=i;
			}
		visited[nextnode]=1;
		for(i=0;i < n;i++)
			if(!visited[i])
				if(mindistance+cost[nextnode][i] < distance[i])
				{
					distance[i]=mindistance+cost[nextnode][i];
					pred[i]=nextnode;
				}
			count++;
	}

	for(i=0;i < n;i++)
		if(i!=startnode)
		{
			printf("\nDistance of %d = %d", i, distance[i]);
			printf("\nPath = %d", i);
			j=i;
			do
			{
				j=pred[j];
				printf(" <-%d", j);
			}
			while(j!=startnode);
		}
}

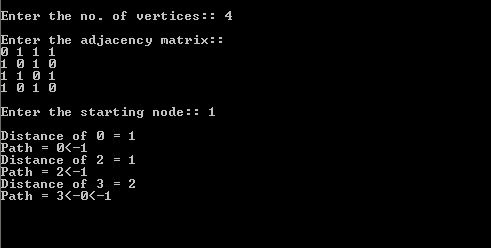
output

---