B-Tree

The B-tree is a generalization of a binary search tree in that a node can have more than two children.
B-tree of order m is a tree which satisfies the following properties:
1. The root has atleast two child.
2. Every node has at most m children.
3. Every non-leaf node (except root) has at least [m/2] children.
4. A non-leaf node with k children contains k−1 keys.
5. All leaves appear in the same level, and carry information.

---

height of a B-tree

Let n = the number of keys in T, n>=1, t>=2,
h = height of T. Then,

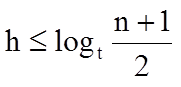
Let T be of height h. The number of nodes is minimized when root has 1 key and all other nodes have t–1 keys.
This gives us 2t^(i-1) nodes at depth i, 1<=i<=h, and 1 node at depth 0. Hence,

---

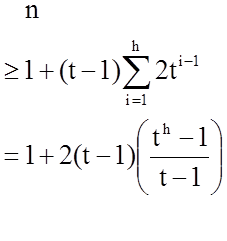
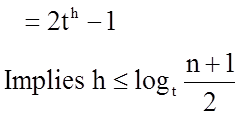
Operations on B-trees

1. B-TREE CREATE
2. B-TREE-INSERT
3. B-TREE-DELETE
4. B-TREE-SEARCH