Creation of B-Tree

To create a nonempty tree, first create an empty tree, then insert nodes.

B-TREE-CREATE(T)

1 x ← ALLOCATE-NODE()

2 leaf[x] ← TRUE

3 n[x] ← 0

4 DISK-WRITE(x)

5 root[T] ← x

Insertion key element into a b-tree

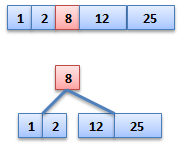
Splitting is fundamental to insert.
Applied to a “full” child of a “nonfull” parent. “full”=2t–1 keys.
for t=4

---

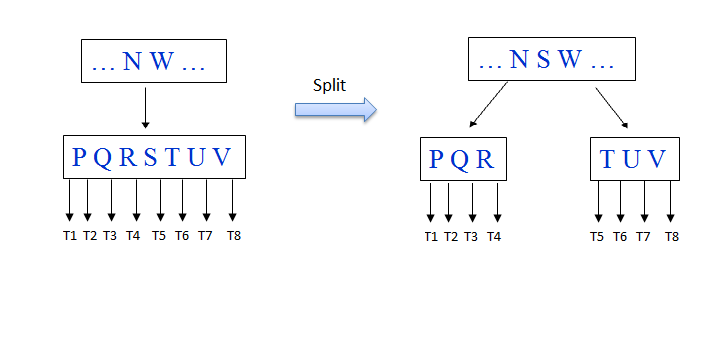
Algorithm For Spliting a node in B-Tree

---

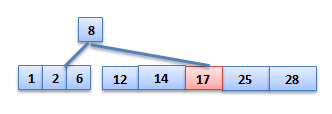
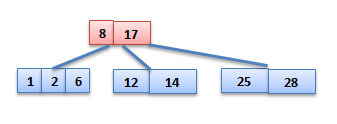
Insert Key value into the tree

Algorithm for insertion

B-TREE-INSERT(T, k)

1 r ← root[T]

2 if n[r] = 2t - 1

3 	then s ← ALLOCATE-NODE()

4 		root[T] ← s

5 		leaf[s] ← FALSE

6 		n[s] ← 0

7 		c1[s] ← r

8 		B-TREE-SPLIT-CHILD(s, 1, r)

9 		B-TREE-INSERT-NONFULL(s, k)

10 	else B-TREE-INSERT-NONFULL(r, k)

Algorithm for B-TREE-INSERT-NONFULL

B-TREE-INSERT-NONFULL(x, k)

1 i ← n[x]

2 if leaf[x]

3 	then while i ≥ 1 and k < keyi[x]

4 		do keyi+1[x] ← keyi[x]

5 			i ← i - 1

6 		keyi+1[x] ← k

7 		n[x] ← n[x] + 1

8 		DISK-WRITE(x)

9 	else while i ≥ 1 and k < keyi[x]

10 		do i ← i - 1

11 	i ← i + 1

12 	DISK-READ(ci[x])

13 	if n[ci[x]] = 2t - 1

14 		then B-TREE-SPLIT-CHILD(x, i, ci[x])

15 			if k> keyi[x]

16 				then i ← i + 1

17 	B-TREE-INSERT-NONFULL(ci[x], k)

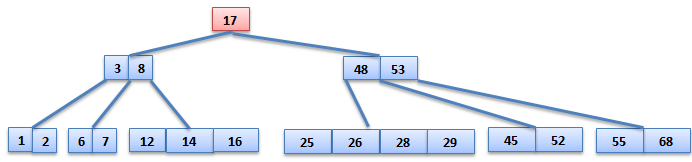
Example
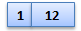
key :- 1,12,8,2,25,6,14,28,17,7,52,16,48,68,3,26,29,53,55,45,67.
Order = 5
Procedure for adding key in b-tree
Step1. Add first key as root node.
Step2. Add next key at the appropriate place in sorted order.
Step3. Same process applied until root node full. if root node full then spliting process applied.
Some importent steps