calculate pow(x,n)
Write a program to calculate pow(x,n)
Given two integers x and n, write a function to compute xn. We may assume that x and n are small and overflow doesn’t happen.
Examples :
Input : x = 2, n = 3 Output : 8 Input : x = 7, n = 2 Output : 49
Below solution divides the problem into subproblems of size y/2 and call the subproblems recursively.
C
#include<stdio.h> /* Function to calculate x raised to the power y */int power(int x, unsigned int y) { if (y == 0) return 1; else if (y%2 == 0) return power(x, y/2)*power(x, y/2); else return x*power(x, y/2)*power(x, y/2); } /* Program to test function power */int main() { int x = 2; unsigned int y = 3; printf("%d", power(x, y)); return 0; } |
Java
class GFG { /* Function to calculate x raised to the power y */ static int power(int x, int y) { if (y == 0) return 1; else if (y % 2 == 0) return power(x, y / 2) * power(x, y / 2); else return x * power(x, y / 2) * power(x, y / 2); } /* Program to test function power */ public static void main(String[] args) { int x = 2; int y = 3; System.out.printf("%d", power(x, y)); } } // This code is contributed by Smitha Dinesh Semwal |
Python3
# Python3 program to calculate pow(x,n) # Function to calculate x # raised to the power y def power(x, y): if (y == 0): return 1 elif (int(y % 2) == 0): return (power(x, int(y / 2)) * power(x, int(y / 2))) else: return (x * power(x, int(y / 2)) * power(x, int(y / 2))) # Driver Code x = 2; y = 3print(power(x, y)) # This code is contributed by Smitha Dinesh Semwal. |
C#
using System; public class GFG { // Function to calculate x raised to the power y static int power(int x, int y) { if (y == 0) return 1; else if (y % 2 == 0) return power(x, y / 2) * power(x, y / 2); else return x * power(x, y / 2) * power(x, y / 2); } // Program to test function power public static void Main() { int x = 2; int y = 3; Console.Write(power(x, y)); } } // This code is contributed by shiv_bhakt. |
PHP
<?php // Function to calculate x // raised to the power y function power($x, $y) { if ($y == 0) return 1; else if ($y % 2 == 0) return power($x, (int)$y / 2) * power($x, (int)$y / 2); else return $x * power($x, (int)$y / 2) * power($x, (int)$y / 2); } // Driver Code $x = 2; $y = 3; echo power($x, $y); // This code is contributed by ajit ?> |
Output :
8
Time Complexity: O(n)
Space Complexity: O(1)
Algorithmic Paradigm: Divide and conquer.
Above function can be optimized to O(logn) by calculating power(x, y/2) only once and storing it.
/* Function to calculate x raised to the power y in O(logn)*/int power(int x, unsigned int y) { int temp; if( y == 0) return 1; temp = power(x, y/2); if (y%2 == 0) return temp*temp; else return x*temp*temp; } |
Time Complexity of optimized solution: O(logn)
Let us extend the pow function to work for negative y and float x.
C
/* Extended version of power function that can work for float x and negative y*/#include<stdio.h> float power(float x, int y) { float temp; if( y == 0) return 1; temp = power(x, y/2); if (y%2 == 0) return temp*temp; else { if(y > 0) return x*temp*temp; else return (temp*temp)/x; } } /* Program to test function power */int main() { float x = 2; int y = -3; printf("%f", power(x, y)); return 0; } |
Java
/* Java code for extended version of power function that can work for float x and negative y */class GFG { static float power(float x, int y) { float temp; if( y == 0) return 1; temp = power(x, y/2); if (y%2 == 0) return temp*temp; else { if(y > 0) return x * temp * temp; else return (temp * temp) / x; } } /* Program to test function power */ public static void main(String[] args) { float x = 2; int y = -3; System.out.printf("%f", power(x, y)); } } // This code is contributed by Smitha Dinesh Semwal. |
Python3
# Python3 code for extended version # of power function that can work # for float x and negative y def power(x, y): if(y == 0): return 1 temp = power(x, int(y / 2)) if (y % 2 == 0): return temp * temp else: if(y > 0): return x * temp * temp else: return (temp * temp) / x # Driver Code x, y = 2, -3print('%.6f' %(power(x, y))) # This code is contributed by Smitha Dinesh Semwal. |
C#
// C# code for extended version of power function // that can work for float x and negative y using System; public class GFG{ static float power(float x, int y) { float temp; if( y == 0) return 1; temp = power(x, y/2); if (y % 2 == 0) return temp * temp; else { if(y > 0) return x * temp * temp; else return (temp * temp) / x; } } // Program to test function power public static void Main() { float x = 2; int y = -3; Console.Write(power(x, y)); } } // This code is contributed by shiv_bhakt. |
PHP
<?php // Extended version of power // function that can work // for float x and negative y function power($x, $y) { $temp; if( $y == 0) return 1; $temp = power($x, $y / 2); if ($y % 2 == 0) return $temp * $temp; else { if($y > 0) return $x * $temp * $temp; else return ($temp * $temp) / $x; } } // Driver Code $x = 2; $y = -3; echo power($x, $y); // This code is contributed by ajit ?> |
Output :
0.125000
Divide and Conquer
Divide and Conquer
Like Greedy and Dynamic Programming, Divide and Conquer is an algorithmic paradigm. A typical Divide and Conquer algorithm solves a problem using following three steps.
1. Divide: Break the given problem into subproblems of same type.
2. Conquer: Recursively solve these subproblems
3. Combine: Appropriately combine the answers
Following are some standard algorithms that are Divide and Conquer algorithms.
1) Binary Search is a searching algorithm. In each step, the algorithm compares the input element x with the value of the middle element in array. If the values match, return the index of middle. Otherwise, if x is less than the middle element, then the algorithm recurs for left side of middle element, else recurs for right side of middle element.
2) Quicksort is a sorting algorithm. The algorithm picks a pivot element, rearranges the array elements in such a way that all elements smaller than the picked pivot element move to left side of pivot, and all greater elements move to right side. Finally, the algorithm recursively sorts the subarrays on left and right of pivot element.
3) Merge Sort is also a sorting algorithm. The algorithm divides the array in two halves, recursively sorts them and finally merges the two sorted halves.
4) Closest Pair of Points The problem is to find the closest pair of points in a set of points in x-y plane. The problem can be solved in O(n^2) time by calculating distances of every pair of points and comparing the distances to find the minimum. The Divide and Conquer algorithm solves the problem in O(nLogn) time.
5) Strassen’s Algorithm is an efficient algorithm to multiply two matrices. A simple method to multiply two matrices need 3 nested loops and is O(n^3). Strassen’s algorithm multiplies two matrices in O(n^2.8974) time.
6) Cooley–Tukey Fast Fourier Transform (FFT) algorithm is the most common algorithm for FFT. It is a divide and conquer algorithm which works in O(nlogn) time.
7) Karatsuba algorithm for fast multiplication it does multiplication of two n-digit numbers in at most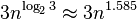 
single-digit multiplications in general (and exactly 
when n is a power of 2). It is therefore faster than the classical algorithm, which requires n2 single-digit products. If n = 210 = 1024, in particular, the exact counts are 310 = 59,049 and (210)2 = 1,048,576, respectively.
We will publishing above algorithms in separate posts.
Divide and Conquer (D & C) vs Dynamic Programming (DP)
Both paradigms (D & C and DP) divide the given problem into subproblems and solve subproblems. How to choose one of them for a given problem? Divide and Conquer should be used when same subproblems are not evaluated many times. Otherwise Dynamic Programming or Memoization should be used. For example, Binary Search is a Divide and Conquer algorithm, we never evaluate the same subproblems again. On the other hand, for calculating nth Fibonacci number, Dynamic Programming should be preferred .
References
Algorithms by Sanjoy Dasgupta, Christos Papadimitriou, Umesh Vazirani
Introduction to Algorithms by Clifford Stein, Thomas H. Cormen, Charles E. Leiserson, Ronald L.
http://en.wikipedia.org/wiki/Karatsuba_algorithm
Solving Cryptarithmetic Puzzles
Solving Cryptarithmetic Puzzles | Backtracking
Newspapers and magazines often have crypt-arithmetic puzzles of the form:
SEND + MORE -------- MONEY --------
The goal here is to assign each letter a digit from 0 to 9 so that the arithmetic works out correctly. The rules are that all occurrences of a letter must be assigned the same digit, and no digit can be assigned to more than one letter.
-
- First, create a list of all the characters that need assigning to pass to Solve
- If all characters are assigned, return true if puzzle is solved, false otherwise
- Otherwise, consider the first unassigned character
- for (every possible choice among the digits not in use)
make that choice and then recursively try to assign the rest of the characters
if recursion sucessful, return true
if !successful, unmake assignment and try another digit
- If all digits have been tried and nothing worked, return false to trigger backtracking
/* ExhaustiveSolve
* ---------------
* This is the "not-very-smart" version of cryptarithmetic solver. It takes
* the puzzle itself (with the 3 strings for the two addends and sum) and a
* string of letters as yet unassigned. If no more letters to assign
* then we've hit a base-case, if the current letter-to-digit mapping solves
* the puzzle, we're done, otherwise we return false to trigger backtracking
* If we have letters to assign, we take the first letter from that list, and
* try assigning it the digits from 0 to 9 and then recursively working
* through solving puzzle from here. If we manage to make a good assignment
* that works, we've succeeded, else we need to unassign that choice and try
* another digit. This version is easy to write, since it uses a simple
* approach (quite similar to permutations if you think about it) but it is
* not so smart because it doesn't take into account the structure of the
* puzzle constraints (for example, once the two digits for the addends have
* been assigned, there is no reason to try anything other than the correct
* digit for the sum) yet it tries a lot of useless combos regardless
*/
bool ExhaustiveSolve(puzzleT puzzle, string lettersToAssign)
{
if (lettersToAssign.empty()) // no more choices to make
return PuzzleSolved(puzzle); // checks arithmetic to see if works
for (int digit = 0; digit <= 9; digit++) // try all digits
{
if (AssignLetterToDigit(lettersToAssign[0], digit))
{
if (ExhaustiveSolve(puzzle, lettersToAssign.substr(1)))
return true;
UnassignLetterFromDigit(lettersToAssign[0], digit);
}
}
return false; // nothing worked, need to backtrack
}
The algorithm above actually has a lot in common with the permutations algorithm, it pretty much just creates all arrangements of the mapping from characters to digits and tries each until one works or all have been successfully tried. For a large puzzle, this could take a while.
A smarter algorithm could take into account the structure of the puzzle and avoid going down dead-end paths. For example, if we assign the characters starting from the ones place and moving to the left, at each stage, we can verify the correctness of what we have so far before we continue onwards. This definitely complicates the code but leads to a tremendous improvement in efficiency, making it much more feasible to solve large puzzles.
Below pseudocode in this case has more special cases, but the same general design
- Start by examining the rightmost digit of the topmost row, with a carry of 0
- If we are beyond the leftmost digit of the puzzle, return true if no carry, false otherwise
- If we are currently trying to assign a char in one of the addends
If char already assigned, just recur on row beneath this one, adding value into sum
If not assigned, then- for (every possible choice among the digits not in use)
make that choice and then on row beneath this one, if successful, return true
if !successful, unmake assignment and try another digit - return false if no assignment worked to trigger backtracking
- for (every possible choice among the digits not in use)
- Else if trying to assign a char in the sum
- If char assigned & matches correct,
recur on next column to the left with carry, if success return true, - If char assigned & doesn’t match, return false
- If char unassigned & correct digit already used, return false
- If char unassigned & correct digit unused,
assign it and recur on next column to left with carry, if success return true - return false to trigger backtracking
Source:
http://see.stanford.edu/materials/icspacs106b/H19-RecBacktrackExamples.pdf
Tug of War
Tug of War | Backtracking
Given a set of n integers, divide the set in two subsets of n/2 sizes each such that the difference of the sum of two subsets is as minimum as possible. If n is even, then sizes of two subsets must be strictly n/2 and if n is odd, then size of one subset must be (n-1)/2 and size of other subset must be (n+1)/2.
For example, let given set be {3, 4, 5, -3, 100, 1, 89, 54, 23, 20}, the size of set is 10. Output for this set should be {4, 100, 1, 23, 20} and {3, 5, -3, 89, 54}. Both output subsets are of size 5 and sum of elements in both subsets is same (148 and 148).
Let us consider another example where n is odd. Let given set be {23, 45, -34, 12, 0, 98, -99, 4, 189, -1, 4}. The output subsets should be {45, -34, 12, 98, -1} and {23, 0, -99, 4, 189, 4}. The sums of elements in two subsets are 120 and 121 respectively.
The following solution tries every possible subset of half size. If one subset of half size is formed, the remaining elements form the other subset. We initialize current set as empty and one by one build it. There are two possibilities for every element, either it is part of current set, or it is part of the remaining elements (other subset). We consider both possibilities for every element. When the size of current set becomes n/2, we check whether this solutions is better than the best solution available so far. If it is, then we update the best solution.
Following is the implementation for Tug of War problem. It prints the required arrays.
C++
#include <iostream>
#include <stdlib.h>
#include <limits.h>
using namespace std;
// function that tries every possible solution by calling itself recursively
void TOWUtil(int* arr, int n, bool* curr_elements, int no_of_selected_elements,
bool* soln, int* min_diff, int sum, int curr_sum, int curr_position)
{
// checks whether the it is going out of bound
if (curr_position == n)
return;
// checks that the numbers of elements left are not less than the
// number of elements required to form the solution
if ((n/2 - no_of_selected_elements) > (n - curr_position))
return;
// consider the cases when current element is not included in the solution
TOWUtil(arr, n, curr_elements, no_of_selected_elements,
soln, min_diff, sum, curr_sum, curr_position+1);
// add the current element to the solution
no_of_selected_elements++;
curr_sum = curr_sum + arr[curr_position];
curr_elements[curr_position] = true;
// checks if a solution is formed
if (no_of_selected_elements == n/2)
{
// checks if the solution formed is better than the best solution so far
if (abs(sum/2 - curr_sum) < *min_diff)
{
*min_diff = abs(sum/2 - curr_sum);
for (int i = 0; i<n; i++)
soln[i] = curr_elements[i];
}
}
else
{
// consider the cases where current element is included in the solution
TOWUtil(arr, n, curr_elements, no_of_selected_elements, soln,
min_diff, sum, curr_sum, curr_position+1);
}
// removes current element before returning to the caller of this function
curr_elements[curr_position] = false;
}
// main function that generate an arr
void tugOfWar(int *arr, int n)
{
// the boolen array that contains the inclusion and exclusion of an element
// in current set. The number excluded automatically form the other set
bool* curr_elements = new bool[n];
// The inclusion/exclusion array for final solution
bool* soln = new bool[n];
int min_diff = INT_MAX;
int sum = 0;
for (int i=0; i<n; i++)
{
sum += arr[i];
curr_elements[i] = soln[i] = false;
}
// Find the solution using recursive function TOWUtil()
TOWUtil(arr, n, curr_elements, 0, soln, &min_diff, sum, 0, 0);
// Print the solution
cout << "The first subset is: ";
for (int i=0; i<n; i++)
{
if (soln[i] == true)
cout << arr[i] << " ";
}
cout << "\nThe second subset is: ";
for (int i=0; i<n; i++)
{
if (soln[i] == false)
cout << arr[i] << " ";
}
}
// Driver program to test above functions
int main()
{
int arr[] = {23, 45, -34, 12, 0, 98, -99, 4, 189, -1, 4};
int n = sizeof(arr)/sizeof(arr[0]);
tugOfWar(arr, n);
return 0;
}
Java
// Java program for Tug of war
import java.util.*;
import java.lang.*;
import java.io.*;
class TugOfWar
{
public int min_diff;
// function that tries every possible solution
// by calling itself recursively
void TOWUtil(int arr[], int n, boolean curr_elements[],
int no_of_selected_elements, boolean soln[],
int sum, int curr_sum, int curr_position)
{
// checks whether the it is going out of bound
if (curr_position == n)
return;
// checks that the numbers of elements left
// are not less than the number of elements
// required to form the solution
if ((n / 2 - no_of_selected_elements) >
(n - curr_position))
return;
// consider the cases when current element
// is not included in the solution
TOWUtil(arr, n, curr_elements,
no_of_selected_elements, soln, sum,
curr_sum, curr_position+1);
// add the current element to the solution
no_of_selected_elements++;
curr_sum = curr_sum + arr[curr_position];
curr_elements[curr_position] = true;
// checks if a solution is formed
if (no_of_selected_elements == n / 2)
{
// checks if the solution formed is
// better than the best solution so
// far
if (Math.abs(sum / 2 - curr_sum) <
min_diff)
{
min_diff = Math.abs(sum / 2 -
curr_sum);
for (int i = 0; i < n; i++)
soln[i] = curr_elements[i];
}
}
else
{
// consider the cases where current
// element is included in the
// solution
TOWUtil(arr, n, curr_elements,
no_of_selected_elements,
soln, sum, curr_sum,
curr_position + 1);
}
// removes current element before
// returning to the caller of this
// function
curr_elements[curr_position] = false;
}
// main function that generate an arr
void tugOfWar(int arr[])
{
int n = arr.length;
// the boolen array that contains the
// inclusion and exclusion of an element
// in current set. The number excluded
// automatically form the other set
boolean[] curr_elements = new boolean[n];
// The inclusion/exclusion array for
// final solution
boolean[] soln = new boolean[n];
min_diff = Integer.MAX_VALUE;
int sum = 0;
for (int i = 0; i < n; i++)
{
sum += arr[i];
curr_elements[i] = soln[i] = false;
}
// Find the solution using recursive
// function TOWUtil()
TOWUtil(arr, n, curr_elements, 0,
soln, sum, 0, 0);
// Print the solution
System.out.print("The first subset is: ");
for (int i = 0; i < n; i++)
{
if (soln[i] == true)
System.out.print(arr[i] + " ");
}
System.out.print("\nThe second subset is: ");
for (int i = 0; i < n; i++)
{
if (soln[i] == false)
System.out.print(arr[i] + " ");
}
}
// Driver program to test above functions
public static void main (String[] args)
{
int arr[] = {23, 45, -34, 12, 0, 98,
-99, 4, 189, -1, 4};
TugOfWar a = new TugOfWar();
a.tugOfWar(arr);
}
}
// This code is contributed by Chhavi
Output:
The first subset is: 45 -34 12 98 -1 The second subset is: 23 0 -99 4 189 4
Sudoku
Sudoku | Backtracking
Given a partially filled 9×9 2D array ‘grid[9][9]’, the goal is to assign digits (from 1 to 9) to the empty cells so that every row, column, and subgrid of size 3×3 contains exactly one instance of the digits from 1 to 9.
Naive Algorithm
The Naive Algorithm is to generate all possible configurations of numbers from 1 to 9 to fill the empty cells. Try every configuration one by one until the correct configuration is found.
Backtracking Algorithm
Like all other Backtracking problems, we can solve Sudoku by one by one assigning numbers to empty cells. Before assigning a number, we check whether it is safe to assign. We basically check that the same number is not present in the current row, current column and current 3X3 subgrid. After checking for safety, we assign the number, and recursively check whether this assignment leads to a solution or not. If the assignment doesn’t lead to a solution, then we try the next number for the current empty cell. And if none of the number (1 to 9) leads to a solution, we return false.
Find row, col of an unassigned cell
If there is none, return true
For digits from 1 to 9
a) If there is no conflict for digit at row, col
assign digit to row, col and recursively try fill in rest of grid
b) If recursion successful, return true
c) Else, remove digit and try another
If all digits have been tried and nothing worked, return false
Following are C++ and Python implementation for Sudoku problem. It prints the completely filled grid as output.
C/C++
// A Backtracking program in C++ to solve Sudoku problem
#include <stdio.h>
// UNASSIGNED is used for empty cells in sudoku grid
#define UNASSIGNED 0
// N is used for the size of Sudoku grid. Size will be NxN
#define N 9
// This function finds an entry in grid that is still unassigned
bool FindUnassignedLocation(int grid[N][N], int &row, int &col);
// Checks whether it will be legal to assign num to the given row, col
bool isSafe(int grid[N][N], int row, int col, int num);
/* Takes a partially filled-in grid and attempts to assign values to
all unassigned locations in such a way to meet the requirements
for Sudoku solution (non-duplication across rows, columns, and boxes) */
bool SolveSudoku(int grid[N][N])
{
int row, col;
// If there is no unassigned location, we are done
if (!FindUnassignedLocation(grid, row, col))
return true; // success!
// consider digits 1 to 9
for (int num = 1; num <= 9; num++)
{
// if looks promising
if (isSafe(grid, row, col, num))
{
// make tentative assignment
grid[row][col] = num;
// return, if success, yay!
if (SolveSudoku(grid))
return true;
// failure, unmake & try again
grid[row][col] = UNASSIGNED;
}
}
return false; // this triggers backtracking
}
/* Searches the grid to find an entry that is still unassigned. If
found, the reference parameters row, col will be set the location
that is unassigned, and true is returned. If no unassigned entries
remain, false is returned. */
bool FindUnassignedLocation(int grid[N][N], int &row, int &col)
{
for (row = 0; row < N; row++)
for (col = 0; col < N; col++)
if (grid[row][col] == UNASSIGNED)
return true;
return false;
}
/* Returns a boolean which indicates whether an assigned entry
in the specified row matches the given number. */
bool UsedInRow(int grid[N][N], int row, int num)
{
for (int col = 0; col < N; col++)
if (grid[row][col] == num)
return true;
return false;
}
/* Returns a boolean which indicates whether an assigned entry
in the specified column matches the given number. */
bool UsedInCol(int grid[N][N], int col, int num)
{
for (int row = 0; row < N; row++)
if (grid[row][col] == num)
return true;
return false;
}
/* Returns a boolean which indicates whether an assigned entry
within the specified 3x3 box matches the given number. */
bool UsedInBox(int grid[N][N], int boxStartRow, int boxStartCol, int num)
{
for (int row = 0; row < 3; row++)
for (int col = 0; col < 3; col++)
if (grid[row+boxStartRow][col+boxStartCol] == num)
return true;
return false;
}
/* Returns a boolean which indicates whether it will be legal to assign
num to the given row,col location. */
bool isSafe(int grid[N][N], int row, int col, int num)
{
/* Check if 'num' is not already placed in current row,
current column and current 3x3 box */
return !UsedInRow(grid, row, num) &&
!UsedInCol(grid, col, num) &&
!UsedInBox(grid, row - row%3 , col - col%3, num);
}
/* A utility function to print grid */
void printGrid(int grid[N][N])
{
for (int row = 0; row < N; row++)
{
for (int col = 0; col < N; col++)
printf("%2d", grid[row][col]);
printf("\n");
}
}
/* Driver Program to test above functions */
int main()
{
// 0 means unassigned cells
int grid[N][N] = {{3, 0, 6, 5, 0, 8, 4, 0, 0},
{5, 2, 0, 0, 0, 0, 0, 0, 0},
{0, 8, 7, 0, 0, 0, 0, 3, 1},
{0, 0, 3, 0, 1, 0, 0, 8, 0},
{9, 0, 0, 8, 6, 3, 0, 0, 5},
{0, 5, 0, 0, 9, 0, 6, 0, 0},
{1, 3, 0, 0, 0, 0, 2, 5, 0},
{0, 0, 0, 0, 0, 0, 0, 7, 4},
{0, 0, 5, 2, 0, 6, 3, 0, 0}};
if (SolveSudoku(grid) == true)
printGrid(grid);
else
printf("No solution exists");
return 0;
}
Python
# A Backtracking program in Pyhton to solve Sudoku problem
# A Utility Function to print the Grid
def print_grid(arr):
for i in range(9):
for j in range(9):
print arr[i][j],
print ('n')
# Function to Find the entry in the Grid that is still not used
# Searches the grid to find an entry that is still unassigned. If
# found, the reference parameters row, col will be set the location
# that is unassigned, and true is returned. If no unassigned entries
# remain, false is returned.
# 'l' is a list variable that has been passed from the solve_sudoku function
# to keep track of incrementation of Rows and Columns
def find_empty_location(arr,l):
for row in range(9):
for col in range(9):
if(arr[row][col]==0):
l[0]=row
l[1]=col
return True
return False
# Returns a boolean which indicates whether any assigned entry
# in the specified row matches the given number.
def used_in_row(arr,row,num):
for i in range(9):
if(arr[row][i] == num):
return True
return False
# Returns a boolean which indicates whether any assigned entry
# in the specified column matches the given number.
def used_in_col(arr,col,num):
for i in range(9):
if(arr[i][col] == num):
return True
return False
# Returns a boolean which indicates whether any assigned entry
# within the specified 3x3 box matches the given number
def used_in_box(arr,row,col,num):
for i in range(3):
for j in range(3):
if(arr[i+row][j+col] == num):
return True
return False
# Checks whether it will be legal to assign num to the given row,col
# Returns a boolean which indicates whether it will be legal to assign
# num to the given row,col location.
def check_location_is_safe(arr,row,col,num):
# Check if 'num' is not already placed in current row,
# current column and current 3x3 box
return not used_in_row(arr,row,num) and not used_in_col(arr,col,num) and not used_in_box(arr,row - row%3,col - col%3,num)
# Takes a partially filled-in grid and attempts to assign values to
# all unassigned locations in such a way to meet the requirements
# for Sudoku solution (non-duplication across rows, columns, and boxes)
def solve_sudoku(arr):
# 'l' is a list variable that keeps the record of row and col in find_empty_location Function
l=[0,0]
# If there is no unassigned location, we are done
if(not find_empty_location(arr,l)):
return True
# Assigning list values to row and col that we got from the above Function
row=l[0]
col=l[1]
# consider digits 1 to 9
for num in range(1,10):
# if looks promising
if(check_location_is_safe(arr,row,col,num)):
# make tentative assignment
arr[row][col]=num
# return, if sucess, ya!
if(solve_sudoku(arr)):
return True
# failure, unmake & try again
arr[row][col] = 0
# this triggers backtracking
return False
# Driver main function to test above functions
if __name__=="__main__":
# creating a 2D array for the grid
grid=[[0 for x in range(9)]for y in range(9)]
# assigning values to the grid
grid=[[3,0,6,5,0,8,4,0,0],
[5,2,0,0,0,0,0,0,0],
[0,8,7,0,0,0,0,3,1],
[0,0,3,0,1,0,0,8,0],
[9,0,0,8,6,3,0,0,5],
[0,5,0,0,9,0,6,0,0],
[1,3,0,0,0,0,2,5,0],
[0,0,0,0,0,0,0,7,4],
[0,0,5,2,0,6,3,0,0]]
# if sucess print the grid
if(solve_sudoku(grid)):
print_grid(grid)
else:
print "No solution exists"
# The above code has been contributed by Harshit Sidhwa.
Output:
3 1 6 5 7 8 4 9 2 5 2 9 1 3 4 7 6 8 4 8 7 6 2 9 5 3 1 2 6 3 4 1 5 9 8 7 9 7 4 8 6 3 1 2 5 8 5 1 7 9 2 6 4 3 1 3 8 9 4 7 2 5 6 6 9 2 3 5 1 8 7 4 7 4 5 2 8 6 3 1 9
References:
http://see.stanford.edu/materials/icspacs106b/H19-RecBacktrackExamples.pdf
Hamiltonian Cycle
Hamiltonian Cycle
Hamiltonian Path in an undirected graph is a path that visits each vertex exactly once. A Hamiltonian cycle (or Hamiltonian circuit) is a Hamiltonian Path such that there is an edge (in graph) from the last vertex to the first vertex of the Hamiltonian Path. Determine whether a given graph contains Hamiltonian Cycle or not. If it contains, then print the path. Following are the input and output of the required function.
Input:
A 2D array graph[V][V] where V is the number of vertices in graph and graph[V][V] is adjacency matrix representation of the graph. A value graph[i][j] is 1 if there is a direct edge from i to j, otherwise graph[i][j] is 0.
Output:
An array path[V] that should contain the Hamiltonian Path. path[i] should represent the ith vertex in the Hamiltonian Path. The code should also return false if there is no Hamiltonian Cycle in the graph.
For example, a Hamiltonian Cycle in the following graph is {0, 1, 2, 4, 3, 0}. There are more Hamiltonian Cycles in the graph like {0, 3, 4, 2, 1, 0}
(0)--(1)--(2) | / \ | | / \ | | / \ | (3)-------(4)
And the following graph doesn’t contain any Hamiltonian Cycle.
(0)--(1)--(2) | / \ | | / \ | | / \ | (3) (4)
Naive Algorithm
Generate all possible configurations of vertices and print a configuration that satisfies the given constraints. There will be n! (n factorial) configurations.
while there are untried conflagrations
{
generate the next configuration
if ( there are edges between two consecutive vertices of this
configuration and there is an edge from the last vertex to
the first ).
{
print this configuration;
break;
}
}
Backtracking Algorithm
Create an empty path array and add vertex 0 to it. Add other vertices, starting from the vertex 1. Before adding a vertex, check for whether it is adjacent to the previously added vertex and not already added. If we find such a vertex, we add the vertex as part of the solution. If we do not find a vertex then we return false.
Implementation of Backtracking solution
Following are implementations of the Backtracking solution.
C/C++
/* C/C++ program for solution of Hamiltonian Cycle problem
using backtracking */
#include<stdio.h>
// Number of vertices in the graph
#define V 5
void printSolution(int path[]);
/* A utility function to check if the vertex v can be added at
index 'pos' in the Hamiltonian Cycle constructed so far (stored
in 'path[]') */
bool isSafe(int v, bool graph[V][V], int path[], int pos)
{
/* Check if this vertex is an adjacent vertex of the previously
added vertex. */
if (graph [ path[pos-1] ][ v ] == 0)
return false;
/* Check if the vertex has already been included.
This step can be optimized by creating an array of size V */
for (int i = 0; i < pos; i++)
if (path[i] == v)
return false;
return true;
}
/* A recursive utility function to solve hamiltonian cycle problem */
bool hamCycleUtil(bool graph[V][V], int path[], int pos)
{
/* base case: If all vertices are included in Hamiltonian Cycle */
if (pos == V)
{
// And if there is an edge from the last included vertex to the
// first vertex
if ( graph[ path[pos-1] ][ path[0] ] == 1 )
return true;
else
return false;
}
// Try different vertices as a next candidate in Hamiltonian Cycle.
// We don't try for 0 as we included 0 as starting point in in hamCycle()
for (int v = 1; v < V; v++)
{
/* Check if this vertex can be added to Hamiltonian Cycle */
if (isSafe(v, graph, path, pos))
{
path[pos] = v;
/* recur to construct rest of the path */
if (hamCycleUtil (graph, path, pos+1) == true)
return true;
/* If adding vertex v doesn't lead to a solution,
then remove it */
path[pos] = -1;
}
}
/* If no vertex can be added to Hamiltonian Cycle constructed so far,
then return false */
return false;
}
/* This function solves the Hamiltonian Cycle problem using Backtracking.
It mainly uses hamCycleUtil() to solve the problem. It returns false
if there is no Hamiltonian Cycle possible, otherwise return true and
prints the path. Please note that there may be more than one solutions,
this function prints one of the feasible solutions. */
bool hamCycle(bool graph[V][V])
{
int *path = new int[V];
for (int i = 0; i < V; i++)
path[i] = -1;
/* Let us put vertex 0 as the first vertex in the path. If there is
a Hamiltonian Cycle, then the path can be started from any point
of the cycle as the graph is undirected */
path[0] = 0;
if ( hamCycleUtil(graph, path, 1) == false )
{
printf("\nSolution does not exist");
return false;
}
printSolution(path);
return true;
}
/* A utility function to print solution */
void printSolution(int path[])
{
printf ("Solution Exists:"
" Following is one Hamiltonian Cycle \n");
for (int i = 0; i < V; i++)
printf(" %d ", path[i]);
// Let us print the first vertex again to show the complete cycle
printf(" %d ", path[0]);
printf("\n");
}
// driver program to test above function
int main()
{
/* Let us create the following graph
(0)--(1)--(2)
| / \ |
| / \ |
| / \ |
(3)-------(4) */
bool graph1[V][V] = {{0, 1, 0, 1, 0},
{1, 0, 1, 1, 1},
{0, 1, 0, 0, 1},
{1, 1, 0, 0, 1},
{0, 1, 1, 1, 0},
};
// Print the solution
hamCycle(graph1);
/* Let us create the following graph
(0)--(1)--(2)
| / \ |
| / \ |
| / \ |
(3) (4) */
bool graph2[V][V] = {{0, 1, 0, 1, 0},
{1, 0, 1, 1, 1},
{0, 1, 0, 0, 1},
{1, 1, 0, 0, 0},
{0, 1, 1, 0, 0},
};
// Print the solution
hamCycle(graph2);
return 0;
}
Java
/* Java program for solution of Hamiltonian Cycle problem
using backtracking */
class HamiltonianCycle
{
final int V = 5;
int path[];
/* A utility function to check if the vertex v can be
added at index 'pos'in the Hamiltonian Cycle
constructed so far (stored in 'path[]') */
boolean isSafe(int v, int graph[][], int path[], int pos)
{
/* Check if this vertex is an adjacent vertex of
the previously added vertex. */
if (graph[path[pos - 1]][v] == 0)
return false;
/* Check if the vertex has already been included.
This step can be optimized by creating an array
of size V */
for (int i = 0; i < pos; i++)
if (path[i] == v)
return false;
return true;
}
/* A recursive utility function to solve hamiltonian
cycle problem */
boolean hamCycleUtil(int graph[][], int path[], int pos)
{
/* base case: If all vertices are included in
Hamiltonian Cycle */
if (pos == V)
{
// And if there is an edge from the last included
// vertex to the first vertex
if (graph[path[pos - 1]][path[0]] == 1)
return true;
else
return false;
}
// Try different vertices as a next candidate in
// Hamiltonian Cycle. We don't try for 0 as we
// included 0 as starting point in in hamCycle()
for (int v = 1; v < V; v++)
{
/* Check if this vertex can be added to Hamiltonian
Cycle */
if (isSafe(v, graph, path, pos))
{
path[pos] = v;
/* recur to construct rest of the path */
if (hamCycleUtil(graph, path, pos + 1) == true)
return true;
/* If adding vertex v doesn't lead to a solution,
then remove it */
path[pos] = -1;
}
}
/* If no vertex can be added to Hamiltonian Cycle
constructed so far, then return false */
return false;
}
/* This function solves the Hamiltonian Cycle problem using
Backtracking. It mainly uses hamCycleUtil() to solve the
problem. It returns false if there is no Hamiltonian Cycle
possible, otherwise return true and prints the path.
Please note that there may be more than one solutions,
this function prints one of the feasible solutions. */
int hamCycle(int graph[][])
{
path = new int[V];
for (int i = 0; i < V; i++)
path[i] = -1;
/* Let us put vertex 0 as the first vertex in the path.
If there is a Hamiltonian Cycle, then the path can be
started from any point of the cycle as the graph is
undirected */
path[0] = 0;
if (hamCycleUtil(graph, path, 1) == false)
{
System.out.println("\nSolution does not exist");
return 0;
}
printSolution(path);
return 1;
}
/* A utility function to print solution */
void printSolution(int path[])
{
System.out.println("Solution Exists: Following" +
" is one Hamiltonian Cycle");
for (int i = 0; i < V; i++)
System.out.print(" " + path[i] + " ");
// Let us print the first vertex again to show the
// complete cycle
System.out.println(" " + path[0] + " ");
}
// driver program to test above function
public static void main(String args[])
{
HamiltonianCycle hamiltonian =
new HamiltonianCycle();
/* Let us create the following graph
(0)--(1)--(2)
| / \ |
| / \ |
| / \ |
(3)-------(4) */
int graph1[][] = {{0, 1, 0, 1, 0},
{1, 0, 1, 1, 1},
{0, 1, 0, 0, 1},
{1, 1, 0, 0, 1},
{0, 1, 1, 1, 0},
};
// Print the solution
hamiltonian.hamCycle(graph1);
/* Let us create the following graph
(0)--(1)--(2)
| / \ |
| / \ |
| / \ |
(3) (4) */
int graph2[][] = {{0, 1, 0, 1, 0},
{1, 0, 1, 1, 1},
{0, 1, 0, 0, 1},
{1, 1, 0, 0, 0},
{0, 1, 1, 0, 0},
};
// Print the solution
hamiltonian.hamCycle(graph2);
}
}
// This code is contributed by Abhishek Shankhadhar
Python
# Python program for solution of
# hamiltonian cycle problem
class Graph():
def __init__(self, vertices):
self.graph = [[0 for column in range(vertices)]\
for row in range(vertices)]
self.V = vertices
''' Check if this vertex is an adjacent vertex
of the previously added vertex and is not
included in the path earlier '''
def isSafe(self, v, pos, path):
# Check if current vertex and last vertex
# in path are adjacent
if self.graph[ path[pos-1] ][v] == 0:
return False
# Check if current vertex not already in path
for vertex in path:
if vertex == v:
return False
return True
# A recursive utility function to solve
# hamiltonian cycle problem
def hamCycleUtil(self, path, pos):
# base case: if all vertices are
# included in the path
if pos == self.V:
# Last vertex must be adjacent to the
# first vertex in path to make a cyle
if self.graph[ path[pos-1] ][ path[0] ] == 1:
return True
else:
return False
# Try different vertices as a next candidate
# in Hamiltonian Cycle. We don't try for 0 as
# we included 0 as starting point in in hamCycle()
for v in range(1,self.V):
if self.isSafe(v, pos, path) == True:
path[pos] = v
if self.hamCycleUtil(path, pos+1) == True:
return True
# Remove current vertex if it doesn't
# lead to a solution
path[pos] = -1
return False
def hamCycle(self):
path = [-1] * self.V
''' Let us put vertex 0 as the first vertex
in the path. If there is a Hamiltonian Cycle,
then the path can be started from any point
of the cycle as the graph is undirected '''
path[0] = 0
if self.hamCycleUtil(path,1) == False:
print "Solution does not exist\n"
return False
self.printSolution(path)
return True
def printSolution(self, path):
print "Solution Exists: Following is one Hamiltonian Cycle"
for vertex in path:
print vertex,
print path[0], "\n"
# Driver Code
''' Let us create the following graph
(0)--(1)--(2)
| / \ |
| / \ |
| / \ |
(3)-------(4) '''
g1 = Graph(5)
g1.graph = [ [0, 1, 0, 1, 0], [1, 0, 1, 1, 1],
[0, 1, 0, 0, 1,],[1, 1, 0, 0, 1],
[0, 1, 1, 1, 0], ]
# Print the solution
g1.hamCycle();
''' Let us create the following graph
(0)--(1)--(2)
| / \ |
| / \ |
| / \ |
(3) (4) '''
g2 = Graph(5)
g2.graph = [ [0, 1, 0, 1, 0], [1, 0, 1, 1, 1],
[0, 1, 0, 0, 1,], [1, 1, 0, 0, 0],
[0, 1, 1, 0, 0], ]
# Print the solution
g2.hamCycle();
# This code is contributed by Divyanshu Mehta
Output:
Solution Exists: Following is one Hamiltonian Cycle 0 1 2 4 3 0 Solution does not exist
Note that the above code always prints cycle starting from 0. Starting point should not matter as cycle can be started from any point. If you want to change the starting point, you should make two changes to above code.
Change “path[0] = 0;” to “path[0] = s;” where s is your new starting point. Also change loop “for (int v = 1; v < V; v++)” in hamCycleUtil() to “for (int v = 0; v < V; v++)”.
m Coloring Problem
m Coloring Problem
Given an undirected graph and a number m, determine if the graph can be colored with at most m colors such that no two adjacent vertices of the graph are colored with same color. Here coloring of a graph means assignment of colors to all vertices.
Input:
1) A 2D array graph[V][V] where V is the number of vertices in graph and graph[V][V] is adjacency matrix representation of the graph. A value graph[i][j] is 1 if there is a direct edge from i to j, otherwise graph[i][j] is 0.
2) An integer m which is maximum number of colors that can be used.
Output:
An array color[V] that should have numbers from 1 to m. color[i] should represent the color assigned to the ith vertex. The code should also return false if the graph cannot be colored with m colors.
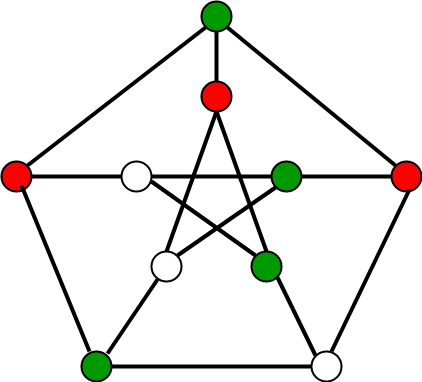
Following is an example of graph that can be colored with 3 different colors.
Naive Algorithm
Generate all possible configurations of colors and print a configuration that satisfies the given constraints.
while there are untried conflagrations
{
generate the next configuration
if no adjacent vertices are colored with same color
{
print this configuration;
}
}
There will be V^m configurations of colors.
Backtracking Algorithm
The idea is to assign colors one by one to different vertices, starting from the vertex 0. Before assigning a color, we check for safety by considering already assigned colors to the adjacent vertices. If we find a color assignment which is safe, we mark the color assignment as part of solution. If we do not a find color due to clashes then we backtrack and return false.
Implementation of Backtracking solution
C/C++
#include<stdio.h>
// Number of vertices in the graph
#define V 4
void printSolution(int color[]);
/* A utility function to check if the current color assignment
is safe for vertex v i.e. checks whether the edge exists or not
(i.e, graph[v][i]==1). If exist then checks whether the color to
be filled in the new vertex(c is sent in the parameter) is already
used by its adjacent vertices(i-->adj vertices) or not (i.e, color[i]==c) */
bool isSafe (int v, bool graph[V][V], int color[], int c)
{
for (int i = 0; i < V; i++)
if (graph[v][i] && c == color[i])
return false;
return true;
}
/* A recursive utility function to solve m coloring problem */
bool graphColoringUtil(bool graph[V][V], int m, int color[], int v)
{
/* base case: If all vertices are assigned a color then
return true */
if (v == V)
return true;
/* Consider this vertex v and try different colors */
for (int c = 1; c <= m; c++)
{
/* Check if assignment of color c to v is fine*/
if (isSafe(v, graph, color, c))
{
color[v] = c;
/* recur to assign colors to rest of the vertices */
if (graphColoringUtil (graph, m, color, v+1) == true)
return true;
/* If assigning color c doesn't lead to a solution
then remove it */
color[v] = 0;
}
}
/* If no color can be assigned to this vertex then return false */
return false;
}
/* This function solves the m Coloring problem using Backtracking.
It mainly uses graphColoringUtil() to solve the problem. It returns
false if the m colors cannot be assigned, otherwise return true and
prints assignments of colors to all vertices. Please note that there
may be more than one solutions, this function prints one of the
feasible solutions.*/
bool graphColoring(bool graph[V][V], int m)
{
// Initialize all color values as 0. This initialization is needed
// correct functioning of isSafe()
int *color = new int[V];
for (int i = 0; i < V; i++)
color[i] = 0;
// Call graphColoringUtil() for vertex 0
if (graphColoringUtil(graph, m, color, 0) == false)
{
printf("Solution does not exist");
return false;
}
// Print the solution
printSolution(color);
return true;
}
/* A utility function to print solution */
void printSolution(int color[])
{
printf("Solution Exists:"
" Following are the assigned colors \n");
for (int i = 0; i < V; i++)
printf(" %d ", color[i]);
printf("\n");
}
// driver program to test above function
int main()
{
/* Create following graph and test whether it is 3 colorable
(3)---(2)
| / |
| / |
| / |
(0)---(1)
*/
bool graph[V][V] = {{0, 1, 1, 1},
{1, 0, 1, 0},
{1, 1, 0, 1},
{1, 0, 1, 0},
};
int m = 3; // Number of colors
graphColoring (graph, m);
return 0;
}
Java
/* Java program for solution of M Coloring problem
using backtracking */
public class mColoringProblem {
final int V = 4;
int color[];
/* A utility function to check if the current
color assignment is safe for vertex v */
boolean isSafe(int v, int graph[][], int color[],
int c)
{
for (int i = 0; i < V; i++)
if (graph[v][i] == 1 && c == color[i])
return false;
return true;
}
/* A recursive utility function to solve m
coloring problem */
boolean graphColoringUtil(int graph[][], int m,
int color[], int v)
{
/* base case: If all vertices are assigned
a color then return true */
if (v == V)
return true;
/* Consider this vertex v and try different
colors */
for (int c = 1; c <= m; c++)
{
/* Check if assignment of color c to v
is fine*/
if (isSafe(v, graph, color, c))
{
color[v] = c;
/* recur to assign colors to rest
of the vertices */
if (graphColoringUtil(graph, m,
color, v + 1))
return true;
/* If assigning color c doesn't lead
to a solution then remove it */
color[v] = 0;
}
}
/* If no color can be assigned to this vertex
then return false */
return false;
}
/* This function solves the m Coloring problem using
Backtracking. It mainly uses graphColoringUtil()
to solve the problem. It returns false if the m
colors cannot be assigned, otherwise return true
and prints assignments of colors to all vertices.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
boolean graphColoring(int graph[][], int m)
{
// Initialize all color values as 0. This
// initialization is needed correct functioning
// of isSafe()
color = new int[V];
for (int i = 0; i < V; i++)
color[i] = 0;
// Call graphColoringUtil() for vertex 0
if (!graphColoringUtil(graph, m, color, 0))
{
System.out.println("Solution does not exist");
return false;
}
// Print the solution
printSolution(color);
return true;
}
/* A utility function to print solution */
void printSolution(int color[])
{
System.out.println("Solution Exists: Following" +
" are the assigned colors");
for (int i = 0; i < V; i++)
System.out.print(" " + color[i] + " ");
System.out.println();
}
// driver program to test above function
public static void main(String args[])
{
mColoringProblem Coloring = new mColoringProblem();
/* Create following graph and test whether it is
3 colorable
(3)---(2)
| / |
| / |
| / |
(0)---(1)
*/
int graph[][] = {{0, 1, 1, 1},
{1, 0, 1, 0},
{1, 1, 0, 1},
{1, 0, 1, 0},
};
int m = 3; // Number of colors
Coloring.graphColoring(graph, m);
}
}
// This code is contributed by Abhishek Shankhadhar
Python
# Python program for solution of M Coloring
# problem using backtracking
class Graph():
def __init__(self, vertices):
self.V = vertices
self.graph = [[0 for column in range(vertices)]\
for row in range(vertices)]
# A utility function to check if the current color assignment
# is safe for vertex v
def isSafe(self, v, colour, c):
for i in range(self.V):
if self.graph[v][i] == 1 and colour[i] == c:
return False
return True
# A recursive utility function to solve m
# coloring problem
def graphColourUtil(self, m, colour, v):
if v == self.V:
return True
for c in range(1, m+1):
if self.isSafe(v, colour, c) == True:
colour[v] = c
if self.graphColourUtil(m, colour, v+1) == True:
return True
colour[v] = 0
def graphColouring(self, m):
colour = [0] * self.V
if self.graphColourUtil(m, colour, 0) == False:
return False
# Print the solution
print "Solution exist and Following are the assigned colours:"
for c in colour:
print c,
return True
# Driver Code
g = Graph(4)
g.graph = [[0,1,1,1], [1,0,1,0], [1,1,0,1], [1,0,1,0]]
m=3
g.graphColouring(m)
# This code is contributed by Divyanshu Mehta
Output:
Solution Exists: Following are the assigned colors 1 2 3 2
References:
http://en.wikipedia.org/wiki/Graph_coloring
Subset Sum
Subset Sum
Subset sum problem is to find subset of elements that are selected from a given set whose sum adds up to a given number K. We are considering the set contains non-negative values. It is assumed that the input set is unique (no duplicates are presented).
Exhaustive Search Algorithm for Subset Sum
One way to find subsets that sum to K is to consider all possible subsets. A power set contains all those subsets generated from a given set. The size of such a power set is 2N.
Backtracking Algorithm for Subset Sum
Using an exhaustive search we consider all subsets irrespective of whether they satisfy given constraints or not. Backtracking can be used to make a systematic consideration of the elements to be selected.
Assume given set of 4 elements, say w[1] … w[4]. Tree diagrams can be used to design backtracking algorithms. The following tree diagram depicts approach of generating variable sized tuple.
In the above tree, a node represents a function call and a branch represents candidate element. The root node contains 4 children. In other words, root considers every element of the set as different branch. The next level sub-trees correspond to the subsets that include the parent node. The branches at each level represent tuple element to be considered. For example, if we are at level 1, tuple_vector[1] can take any value of four branches generated. If we are at level 2 of leftmost node, tuple_vector[2] can take any value of three branches generated, and so on…
For example the left most child of root generates all those subsets that include w[1]. Similarly the second child of root generates all those subsets that includes w[2] and excludes w[1].
As we go down along depth of tree we add elements so far, and if the added sum is satisfying explicit constraints, we will continue to generate child nodes further. Whenever the constraints are not met, we stop further generation of sub-trees of that node, and backtrack to previous node to explore the nodes not yet explored. In many scenarios, it saves considerable amount of processing time.
The tree should trigger a clue to implement the backtracking algorithm (try yourself). It prints all those subsets whose sum add up to given number. We need to explore the nodes along the breadth and depth of the tree. Generating nodes along breadth is controlled by loop and nodes along the depth are generated using recursion (post-order traversal). Pseudo code given below,
if(subset is satisfying the constraint)
print the subset
exclude the current element and consider next element
else
generate the nodes of present level along breadth of tree and
recur for next levels
Following is C implementation of subset sum using variable size tuple vector. Note that the following program explores all possibilities similar to exhaustive search. It is to demonstrate how backtracking can be used. See next code to verify, how we can optimize the backtracking solution.
#include <stdio.h>
#include <stdlib.h>
#define ARRAYSIZE(a) (sizeof(a))/(sizeof(a[0]))
static int total_nodes;
// prints subset found
void printSubset(int A[], int size)
{
for(int i = 0; i < size; i++)
{
printf("%*d", 5, A[i]);
}
printf("n");
}
// inputs
// s - set vector
// t - tuplet vector
// s_size - set size
// t_size - tuplet size so far
// sum - sum so far
// ite - nodes count
// target_sum - sum to be found
void subset_sum(int s[], int t[],
int s_size, int t_size,
int sum, int ite,
int const target_sum)
{
total_nodes++;
if( target_sum == sum )
{
// We found subset
printSubset(t, t_size);
// Exclude previously added item and consider next candidate
subset_sum(s, t, s_size, t_size-1, sum - s[ite], ite + 1, target_sum);
return;
}
else
{
// generate nodes along the breadth
for( int i = ite; i < s_size; i++ )
{
t[t_size] = s[i];
// consider next level node (along depth)
subset_sum(s, t, s_size, t_size + 1, sum + s[i], i + 1, target_sum);
}
}
}
// Wrapper to print subsets that sum to target_sum
// input is weights vector and target_sum
void generateSubsets(int s[], int size, int target_sum)
{
int *tuplet_vector = (int *)malloc(size * sizeof(int));
subset_sum(s, tuplet_vector, size, 0, 0, 0, target_sum);
free(tuplet_vector);
}
int main()
{
int weights[] = {10, 7, 5, 18, 12, 20, 15};
int size = ARRAYSIZE(weights);
generateSubsets(weights, size, 35);
printf("Nodes generated %dn", total_nodes);
return 0;
}
The power of backtracking appears when we combine explicit and implicit constraints, and we stop generating nodes when these checks fail. We can improve the above algorithm by strengthening the constraint checks and presorting the data. By sorting the initial array, we need not to consider rest of the array, once the sum so far is greater than target number. We can backtrack and check other possibilities.
Similarly, assume the array is presorted and we found one subset. We can generate next node excluding the present node only when inclusion of next node satisfies the constraints. Given below is optimized implementation (it prunes the subtree if it is not satisfying contraints).
#include <stdio.h>
#include <stdlib.h>
#define ARRAYSIZE(a) (sizeof(a))/(sizeof(a[0]))
static int total_nodes;
// prints subset found
void printSubset(int A[], int size)
{
for(int i = 0; i < size; i++)
{
printf("%*d", 5, A[i]);
}
printf("n");
}
// qsort compare function
int comparator(const void *pLhs, const void *pRhs)
{
int *lhs = (int *)pLhs;
int *rhs = (int *)pRhs;
return *lhs > *rhs;
}
// inputs
// s - set vector
// t - tuplet vector
// s_size - set size
// t_size - tuplet size so far
// sum - sum so far
// ite - nodes count
// target_sum - sum to be found
void subset_sum(int s[], int t[],
int s_size, int t_size,
int sum, int ite,
int const target_sum)
{
total_nodes++;
if( target_sum == sum )
{
// We found sum
printSubset(t, t_size);
// constraint check
if( ite + 1 < s_size && sum - s[ite] + s[ite+1] <= target_sum )
{
// Exclude previous added item and consider next candidate
subset_sum(s, t, s_size, t_size-1, sum - s[ite], ite + 1, target_sum);
}
return;
}
else
{
// constraint check
if( ite < s_size && sum + s[ite] <= target_sum )
{
// generate nodes along the breadth
for( int i = ite; i < s_size; i++ )
{
t[t_size] = s[i];
if( sum + s[i] <= target_sum )
{
// consider next level node (along depth)
subset_sum(s, t, s_size, t_size + 1, sum + s[i], i + 1, target_sum);
}
}
}
}
}
// Wrapper that prints subsets that sum to target_sum
void generateSubsets(int s[], int size, int target_sum)
{
int *tuplet_vector = (int *)malloc(size * sizeof(int));
int total = 0;
// sort the set
qsort(s, size, sizeof(int), &comparator);
for( int i = 0; i < size; i++ )
{
total += s[i];
}
if( s[0] <= target_sum && total >= target_sum )
{
subset_sum(s, tuplet_vector, size, 0, 0, 0, target_sum);
}
free(tuplet_vector);
}
int main()
{
int weights[] = {15, 22, 14, 26, 32, 9, 16, 8};
int target = 53;
int size = ARRAYSIZE(weights);
generateSubsets(weights, size, target);
printf("Nodes generated %dn", total_nodes);
return 0;
}
As another approach, we can generate the tree in fixed size tuple analogs to the binary pattern. We will kill the sub-trees when the constraints are not satisfied.
N Queen Problem
N Queen Problem
We have discussed Knight’s tour and Rat in a Maze problem. Let us discuss N Queen as another example problem that can be solved using Backtracking.
The N Queen is the problem of placing N chess queens on an N×N chessboard so that no two queens attack each other. For example, following is a solution for 4 Queen problem.
The expected output is a binary matrix which has 1s for the blocks where queens are placed. For example, following is the output matrix for above 4 queen solution.
{ 0, 1, 0, 0}
{ 0, 0, 0, 1}
{ 1, 0, 0, 0}
{ 0, 0, 1, 0}
Naive Algorithm
Generate all possible configurations of queens on board and print a configuration that satisfies the given constraints.
while there are untried configurations
{
generate the next configuration
if queens don't attack in this configuration then
{
print this configuration;
}
}
Backtracking Algorithm
The idea is to place queens one by one in different columns, starting from the leftmost column. When we place a queen in a column, we check for clashes with already placed queens. In the current column, if we find a row for which there is no clash, we mark this row and column as part of the solution. If we do not find such a row due to clashes then we backtrack and return false.
- Start in the leftmost column
- If all queens are placed return true
- Try all rows in the current column. Do following for every tried row.
- if the queen can be placed safely in this row then mark this [row, column] as part of the solution and recursively check if placing queen here leads to a solution.
- If placing the queen in [row, column] leads to a solution then return true.
- If placing queen doesn’t lead to a solution then umark this [row, column] (Backtrack) and go to step (a) to try other rows.
- If all rows have been tried and nothing worked, return false to trigger backtracking.
Implementation of Backtracking solution
C/C++
/* C/C++ program to solve N Queen Problem using
backtracking */
#define N 4
#include<stdio.h>
#include<stdbool.h>
/* A utility function to print solution */
void printSolution(int board[N][N])
{
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
printf(" %d ", board[i][j]);
printf("\n");
}
}
/* A utility function to check if a queen can
be placed on board[row][col]. Note that this
function is called when "col" queens are
already placed in columns from 0 to col -1.
So we need to check only left side for
attacking queens */
bool isSafe(int board[N][N], int row, int col)
{
int i, j;
/* Check this row on left side */
for (i = 0; i < col; i++)
if (board[row][i])
return false;
/* Check upper diagonal on left side */
for (i=row, j=col; i>=0 && j>=0; i--, j--)
if (board[i][j])
return false;
/* Check lower diagonal on left side */
for (i=row, j=col; j>=0 && i<N; i++, j--)
if (board[i][j])
return false;
return true;
}
/* A recursive utility function to solve N
Queen problem */
bool solveNQUtil(int board[N][N], int col)
{
/* base case: If all queens are placed
then return true */
if (col >= N)
return true;
/* Consider this column and try placing
this queen in all rows one by one */
for (int i = 0; i < N; i++)
{
/* Check if the queen can be placed on
board[i][col] */
if ( isSafe(board, i, col) )
{
/* Place this queen in board[i][col] */
board[i][col] = 1;
/* recur to place rest of the queens */
if ( solveNQUtil(board, col + 1) )
return true;
/* If placing queen in board[i][col]
doesn't lead to a solution, then
remove queen from board[i][col] */
board[i][col] = 0; // BACKTRACK
}
}
/* If the queen cannot be placed in any row in
this colum col then return false */
return false;
}
/* This function solves the N Queen problem using
Backtracking. It mainly uses solveNQUtil() to
solve the problem. It returns false if queens
cannot be placed, otherwise, return true and
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
bool solveNQ()
{
int board[N][N] = { {0, 0, 0, 0},
{0, 0, 0, 0},
{0, 0, 0, 0},
{0, 0, 0, 0}
};
if ( solveNQUtil(board, 0) == false )
{
printf("Solution does not exist");
return false;
}
printSolution(board);
return true;
}
// driver program to test above function
int main()
{
solveNQ();
return 0;
}
Java
/* Java program to solve N Queen Problem using
backtracking */
public class NQueenProblem
{
final int N = 4;
/* A utility function to print solution */
void printSolution(int board[][])
{
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
System.out.print(" " + board[i][j]
+ " ");
System.out.println();
}
}
/* A utility function to check if a queen can
be placed on board[row][col]. Note that this
function is called when "col" queens are already
placeed in columns from 0 to col -1. So we need
to check only left side for attacking queens */
boolean isSafe(int board[][], int row, int col)
{
int i, j;
/* Check this row on left side */
for (i = 0; i < col; i++)
if (board[row][i] == 1)
return false;
/* Check upper diagonal on left side */
for (i=row, j=col; i>=0 && j>=0; i--, j--)
if (board[i][j] == 1)
return false;
/* Check lower diagonal on left side */
for (i=row, j=col; j>=0 && i<N; i++, j--)
if (board[i][j] == 1)
return false;
return true;
}
/* A recursive utility function to solve N
Queen problem */
boolean solveNQUtil(int board[][], int col)
{
/* base case: If all queens are placed
then return true */
if (col >= N)
return true;
/* Consider this column and try placing
this queen in all rows one by one */
for (int i = 0; i < N; i++)
{
/* Check if the queen can be placed on
board[i][col] */
if (isSafe(board, i, col))
{
/* Place this queen in board[i][col] */
board[i][col] = 1;
/* recur to place rest of the queens */
if (solveNQUtil(board, col + 1) == true)
return true;
/* If placing queen in board[i][col]
doesn't lead to a solution then
remove queen from board[i][col] */
board[i][col] = 0; // BACKTRACK
}
}
/* If the queen can not be placed in any row in
this colum col, then return false */
return false;
}
/* This function solves the N Queen problem using
Backtracking. It mainly uses solveNQUtil () to
solve the problem. It returns false if queens
cannot be placed, otherwise, return true and
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
boolean solveNQ()
{
int board[][] = {{0, 0, 0, 0},
{0, 0, 0, 0},
{0, 0, 0, 0},
{0, 0, 0, 0}
};
if (solveNQUtil(board, 0) == false)
{
System.out.print("Solution does not exist");
return false;
}
printSolution(board);
return true;
}
// driver program to test above function
public static void main(String args[])
{
NQueenProblem Queen = new NQueenProblem();
Queen.solveNQ();
}
}
// This code is contributed by Abhishek Shankhadhar
Python
# Python program to solve N Queen
# Problem using backtracking
global N
N = 4
def printSolution(board):
for i in range(N):
for j in range(N):
print board[i][j],
print
# A utility function to check if a queen can
# be placed on board[row][col]. Note that this
# function is called when "col" queens are
# already placed in columns from 0 to col -1.
# So we need to check only left side for
# attacking queens
def isSafe(board, row, col):
# Check this row on left side
for i in range(col):
if board[row][i] == 1:
return False
# Check upper diagonal on left side
for i,j in zip(range(row,-1,-1), range(col,-1,-1)):
if board[i][j] == 1:
return False
# Check lower diagonal on left side
for i,j in zip(range(row,N,1), range(col,-1,-1)):
if board[i][j] == 1:
return False
return True
def solveNQUtil(board, col):
# base case: If all queens are placed
# then return true
if col >= N:
return True
# Consider this column and try placing
# this queen in all rows one by one
for i in range(N):
if isSafe(board, i, col):
# Place this queen in board[i][col]
board[i][col] = 1
# recur to place rest of the queens
if solveNQUtil(board, col+1) == True:
return True
# If placing queen in board[i][col
# doesn't lead to a solution, then
# queen from board[i][col]
board[i][col] = 0
# if the queen can not be placed in any row in
# this colum col then return false
return False
# This function solves the N Queen problem using
# Backtracking. It mainly uses solveNQUtil() to
# solve the problem. It returns false if queens
# cannot be placed, otherwise return true and
# placement of queens in the form of 1s.
# note that there may be more than one
# solutions, this function prints one of the
# feasible solutions.
def solveNQ():
board = [ [0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]
]
if solveNQUtil(board, 0) == False:
print "Solution does not exist"
return False
printSolution(board)
return True
# driver program to test above function
solveNQ()
# This code is contributed by Divyanshu Mehta
Output: The 1 values indicate placements of queens
0 0 1 0 1 0 0 0 0 0 0 1 0 1 0 0
Rat in a Maze
Rat in a Maze
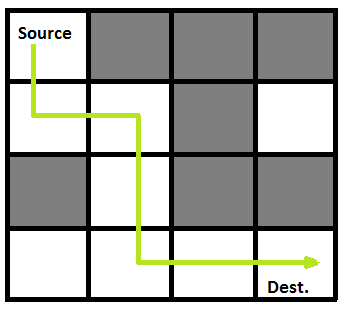
We have discussed Backtracking and Knight’s tour problem in Set 1. Let us discuss Rat in a Maze as another example problem that can be solved using Backtracking.
A Maze is given as N*N binary matrix of blocks where source block is the upper left most block i.e., maze[0][0] and destination block is lower rightmost block i.e., maze[N-1][N-1]. A rat starts from source and has to reach the destination. The rat can move only in two directions: forward and down.
In the maze matrix, 0 means the block is a dead end and 1 means the block can be used in the path from source to destination. Note that this is a simple version of the typical Maze problem. For example, a more complex version can be that the rat can move in 4 directions and a more complex version can be with a limited number of moves.
Following is an example maze.
Gray blocks are dead ends (value = 0).
Following is binary matrix representation of the above maze.
{1, 0, 0, 0}
{1, 1, 0, 1}
{0, 1, 0, 0}
{1, 1, 1, 1}
Following is a maze with highlighted solution path.
Following is the solution matrix (output of program) for the above input matrx.
{1, 0, 0, 0}
{1, 1, 0, 0}
{0, 1, 0, 0}
{0, 1, 1, 1}
All enteries in solution path are marked as 1.
Naive Algorithm
The Naive Algorithm is to generate all paths from source to destination and one by one check if the generated path satisfies the constraints.
while there are untried paths
{
generate the next path
if this path has all blocks as 1
{
print this path;
}
}
Backtracking Algorithm
If destination is reached
print the solution matrix
Else
a) Mark current cell in solution matrix as 1.
b) Move forward in the horizontal direction and recursively check if this
move leads to a solution.
c) If the move chosen in the above step doesn't lead to a solution
then move down and check if this move leads to a solution.
d) If none of the above solutions works then unmark this cell as 0
(BACKTRACK) and return false.
Implementation of Backtracking solution
C/C++
/* C/C++ program to solve Rat in a Maze problem using
backtracking */
#include<stdio.h>
// Maze size
#define N 4
bool solveMazeUtil(int maze[N][N], int x, int y, int sol[N][N]);
/* A utility function to print solution matrix sol[N][N] */
void printSolution(int sol[N][N])
{
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
printf(" %d ", sol[i][j]);
printf("\n");
}
}
/* A utility function to check if x,y is valid index for N*N maze */
bool isSafe(int maze[N][N], int x, int y)
{
// if (x,y outside maze) return false
if(x >= 0 && x < N && y >= 0 && y < N && maze[x][y] == 1)
return true;
return false;
}
/* This function solves the Maze problem using Backtracking. It mainly
uses solveMazeUtil() to solve the problem. It returns false if no
path is possible, otherwise return true and prints the path in the
form of 1s. Please note that there may be more than one solutions,
this function prints one of the feasible solutions.*/
bool solveMaze(int maze[N][N])
{
int sol[N][N] = { {0, 0, 0, 0},
{0, 0, 0, 0},
{0, 0, 0, 0},
{0, 0, 0, 0}
};
if(solveMazeUtil(maze, 0, 0, sol) == false)
{
printf("Solution doesn't exist");
return false;
}
printSolution(sol);
return true;
}
/* A recursive utility function to solve Maze problem */
bool solveMazeUtil(int maze[N][N], int x, int y, int sol[N][N])
{
// if (x,y is goal) return true
if(x == N-1 && y == N-1)
{
sol[x][y] = 1;
return true;
}
// Check if maze[x][y] is valid
if(isSafe(maze, x, y) == true)
{
// mark x,y as part of solution path
sol[x][y] = 1;
/* Move forward in x direction */
if (solveMazeUtil(maze, x+1, y, sol) == true)
return true;
/* If moving in x direction doesn't give solution then
Move down in y direction */
if (solveMazeUtil(maze, x, y+1, sol) == true)
return true;
/* If none of the above movements work then BACKTRACK:
unmark x,y as part of solution path */
sol[x][y] = 0;
return false;
}
return false;
}
// driver program to test above function
int main()
{
int maze[N][N] = { {1, 0, 0, 0},
{1, 1, 0, 1},
{0, 1, 0, 0},
{1, 1, 1, 1}
};
solveMaze(maze);
return 0;
}
Java
/* Java program to solve Rat in a Maze problem using
backtracking */
public class RatMaze
{
final int N = 4;
/* A utility function to print solution matrix
sol[N][N] */
void printSolution(int sol[][])
{
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
System.out.print(" " + sol[i][j] +
" ");
System.out.println();
}
}
/* A utility function to check if x,y is valid
index for N*N maze */
boolean isSafe(int maze[][], int x, int y)
{
// if (x,y outside maze) return false
return (x >= 0 && x < N && y >= 0 &&
y < N && maze[x][y] == 1);
}
/* This function solves the Maze problem using
Backtracking. It mainly uses solveMazeUtil()
to solve the problem. It returns false if no
path is possible, otherwise return true and
prints the path in the form of 1s. Please note
that there may be more than one solutions, this
function prints one of the feasible solutions.*/
boolean solveMaze(int maze[][])
{
int sol[][] = {{0, 0, 0, 0},
{0, 0, 0, 0},
{0, 0, 0, 0},
{0, 0, 0, 0}
};
if (solveMazeUtil(maze, 0, 0, sol) == false)
{
System.out.print("Solution doesn't exist");
return false;
}
printSolution(sol);
return true;
}
/* A recursive utility function to solve Maze
problem */
boolean solveMazeUtil(int maze[][], int x, int y,
int sol[][])
{
// if (x,y is goal) return true
if (x == N - 1 && y == N - 1)
{
sol[x][y] = 1;
return true;
}
// Check if maze[x][y] is valid
if (isSafe(maze, x, y) == true)
{
// mark x,y as part of solution path
sol[x][y] = 1;
/* Move forward in x direction */
if (solveMazeUtil(maze, x + 1, y, sol))
return true;
/* If moving in x direction doesn't give
solution then Move down in y direction */
if (solveMazeUtil(maze, x, y + 1, sol))
return true;
/* If none of the above movements works then
BACKTRACK: unmark x,y as part of solution
path */
sol[x][y] = 0;
return false;
}
return false;
}
public static void main(String args[])
{
RatMaze rat = new RatMaze();
int maze[][] = {{1, 0, 0, 0},
{1, 1, 0, 1},
{0, 1, 0, 0},
{1, 1, 1, 1}
};
rat.solveMaze(maze);
}
}
// This code is contributed by Abhishek Shankhadhar
Python3
# Python3 program to solve Rat in a Maze
# problem using backracking
# Maze size
N = 4
# A utility function to print solution matrix sol
def printSolution( sol ):
for i in sol:
for j in i:
print(str(j) + " ", end="")
print("")
# A utility function to check if x,y is valid
# index for N*N Maze
def isSafe( maze, x, y ):
if x >= 0 and x < N and y >= 0 and y < N and maze[x][y] == 1:
return True
return False
""" This function solves the Maze problem using Backtracking.
It mainly uses solveMazeUtil() to solve the problem. It
returns false if no path is possible, otherwise return
true and prints the path in the form of 1s. Please note
that there may be more than one solutions, this function
prints one of the feasable solutions. """
def solveMaze( maze ):
# Creating a 4 * 4 2-D list
sol = [ [ 0 for j in range(4) ] for i in range(4) ]
if solveMazeUtil(maze, 0, 0, sol) == False:
print("Solution doesn't exist");
return False
printSolution(sol)
return True
# A recursive utility function to solve Maze problem
def solveMazeUtil(maze, x, y, sol):
#if (x,y is goal) return True
if x == N - 1 and y == N - 1:
sol[x][y] = 1
return True
# Check if maze[x][y] is valid
if isSafe(maze, x, y) == True:
# mark x, y as part of solution path
sol[x][y] = 1
# Move forward in x direction
if solveMazeUtil(maze, x + 1, y, sol) == True:
return True
# If moving in x direction doesn't give solution
# then Move down in y direction
if solveMazeUtil(maze, x, y + 1, sol) == True:
return True
# If none of the above movements work then
# BACKTRACK: unmark x,y as part of solution path
sol[x][y] = 0
return False
# Driver program to test above function
if __name__ == "__main__":
# Initialising the maze
maze = [ [1, 0, 0, 0],
[1, 1, 0, 1],
[0, 1, 0, 0],
[1, 1, 1, 1] ]
solveMaze(maze)
# This code is contributed by Shiv Shankar
Output: The 1 values show the path for rat
1 0 0 0 1 1 0 0 0 1 0 0 0 1 1 1