The Knight’s tour problem
Backtracking is an algorithmic paradigm that tries different solutions until finds a solution that “works”. Problems which are typically solved using backtracking technique have the following property in common. These problems can only be solved by trying every possible configuration and each configuration is tried only once. A Naive solution for these problems is to try all configurations and output a configuration that follows given problem constraints. Backtracking works in an incremental way and is an optimization over the Naive solution where all possible configurations are generated and tried.
For example, consider the following Knight’s Tour problem.
The knight is placed on the first block of an empty board and, moving according to the rules of chess, must visit each square exactly once.
Path followed by Knight to cover all the cells
Following is chessboard with 8 x 8 cells. Numbers in cells indicate move number of Knight.
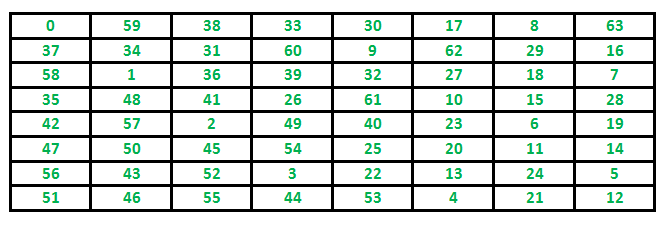
Let us first discuss the Naive algorithm for this problem and then the Backtracking algorithm.
Naive Algorithm for Knight’s tour
The Naive Algorithm is to generate all tours one by one and check if the generated tour satisfies the constraints.
while there are untried tours
{
generate the next tour
if this tour covers all squares
{
print this path;
}
}
Backtracking works in an incremental way to attack problems. Typically, we start from an empty solution vector and one by one add items (Meaning of item varies from problem to problem. In context of Knight’s tour problem, an item is a Knight’s move). When we add an item, we check if adding the current item violates the problem constraint, if it does then we remove the item and try other alternatives. If none of the alternatives work out then we go to the previous stage and remove the item added in the previous stage. If we reach the initial stage back then we say that no solution exists. If adding an item doesn’t violate constraints then we recursively add items one by one. If the solution vector becomes complete then we print the solution.
Backtracking Algorithm for Knight’s tour
Following is the Backtracking algorithm for Knight’s tour problem.
If all squares are visited
print the solution
Else
a) Add one of the next moves to solution vector and recursively
check if this move leads to a solution. (A Knight can make maximum
eight moves. We choose one of the 8 moves in this step).
b) If the move chosen in the above step doesn't lead to a solution
then remove this move from the solution vector and try other
alternative moves.
c) If none of the alternatives work then return false (Returning false
will remove the previously added item in recursion and if false is
returned by the initial call of recursion then "no solution exists" )
Following are implementations for Knight’s tour problem. It prints one of the possible solutions in 2D matrix form. Basically, the output is a 2D 8*8 matrix with numbers from 0 to 63 and these numbers show steps made by Knight.
C
// C program for Knight Tour problem
#include<stdio.h>
#define N 8
int solveKTUtil(int x, int y, int movei, int sol[N][N],
int xMove[], int yMove[]);
/* A utility function to check if i,j are valid indexes
for N*N chessboard */
bool isSafe(int x, int y, int sol[N][N])
{
return ( x >= 0 && x < N && y >= 0 &&
y < N && sol[x][y] == -1);
}
/* A utility function to print solution matrix sol[N][N] */
void printSolution(int sol[N][N])
{
for (int x = 0; x < N; x++)
{
for (int y = 0; y < N; y++)
printf(" %2d ", sol[x][y]);
printf("\n");
}
}
/* This function solves the Knight Tour problem using
Backtracking. This function mainly uses solveKTUtil()
to solve the problem. It returns false if no complete
tour is possible, otherwise return true and prints the
tour.
Please note that there may be more than one solutions,
this function prints one of the feasible solutions. */
bool solveKT()
{
int sol[N][N];
/* Initialization of solution matrix */
for (int x = 0; x < N; x++)
for (int y = 0; y < N; y++)
sol[x][y] = -1;
/* xMove[] and yMove[] define next move of Knight.
xMove[] is for next value of x coordinate
yMove[] is for next value of y coordinate */
int xMove[8] = { 2, 1, -1, -2, -2, -1, 1, 2 };
int yMove[8] = { 1, 2, 2, 1, -1, -2, -2, -1 };
// Since the Knight is initially at the first block
sol[0][0] = 0;
/* Start from 0,0 and explore all tours using
solveKTUtil() */
if (solveKTUtil(0, 0, 1, sol, xMove, yMove) == false)
{
printf("Solution does not exist");
return false;
}
else
printSolution(sol);
return true;
}
/* A recursive utility function to solve Knight Tour
problem */
int solveKTUtil(int x, int y, int movei, int sol[N][N],
int xMove[N], int yMove[N])
{
int k, next_x, next_y;
if (movei == N*N)
return true;
/* Try all next moves from the current coordinate x, y */
for (k = 0; k < 8; k++)
{
next_x = x + xMove[k];
next_y = y + yMove[k];
if (isSafe(next_x, next_y, sol))
{
sol[next_x][next_y] = movei;
if (solveKTUtil(next_x, next_y, movei+1, sol,
xMove, yMove) == true)
return true;
else
sol[next_x][next_y] = -1;// backtracking
}
}
return false;
}
/* Driver program to test above functions */
int main()
{
solveKT();
return 0;
}
Java
// Java program for Knight Tour problem
class KnightTour {
static int N = 8;
/* A utility function to check if i,j are
valid indexes for N*N chessboard */
static boolean isSafe(int x, int y, int sol[][]) {
return (x >= 0 && x < N && y >= 0 &&
y < N && sol[x][y] == -1);
}
/* A utility function to print solution
matrix sol[N][N] */
static void printSolution(int sol[][]) {
for (int x = 0; x < N; x++) {
for (int y = 0; y < N; y++)
System.out.print(sol[x][y] + " ");
System.out.println();
}
}
/* This function solves the Knight Tour problem
using Backtracking. This function mainly
uses solveKTUtil() to solve the problem. It
returns false if no complete tour is possible,
otherwise return true and prints the tour.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions. */
static boolean solveKT() {
int sol[][] = new int[8][8];
/* Initialization of solution matrix */
for (int x = 0; x < N; x++)
for (int y = 0; y < N; y++)
sol[x][y] = -1;
/* xMove[] and yMove[] define next move of Knight.
xMove[] is for next value of x coordinate
yMove[] is for next value of y coordinate */
int xMove[] = {2, 1, -1, -2, -2, -1, 1, 2};
int yMove[] = {1, 2, 2, 1, -1, -2, -2, -1};
// Since the Knight is initially at the first block
sol[0][0] = 0;
/* Start from 0,0 and explore all tours using
solveKTUtil() */
if (!solveKTUtil(0, 0, 1, sol, xMove, yMove)) {
System.out.println("Solution does not exist");
return false;
} else
printSolution(sol);
return true;
}
/* A recursive utility function to solve Knight
Tour problem */
static boolean solveKTUtil(int x, int y, int movei,
int sol[][], int xMove[],
int yMove[]) {
int k, next_x, next_y;
if (movei == N * N)
return true;
/* Try all next moves from the current coordinate
x, y */
for (k = 0; k < 8; k++) {
next_x = x + xMove[k];
next_y = y + yMove[k];
if (isSafe(next_x, next_y, sol)) {
sol[next_x][next_y] = movei;
if (solveKTUtil(next_x, next_y, movei + 1,
sol, xMove, yMove))
return true;
else
sol[next_x][next_y] = -1;// backtracking
}
}
return false;
}
/* Driver program to test above functions */
public static void main(String args[]) {
solveKT();
}
}
// This code is contributed by Abhishek Shankhadhar
C#
// C# program for
// Knight Tour problem
using System;
class GFG
{
static int N = 8;
/* A utility function to
check if i,j are valid
indexes for N*N chessboard */
static bool isSafe(int x, int y,
int[,] sol)
{
return (x >= 0 && x < N &&
y >= 0 && y < N &&
sol[x, y] == -1);
}
/* A utility function to
print solution matrix sol[N][N] */
static void printSolution(int[,] sol)
{
for (int x = 0; x < N; x++)
{
for (int y = 0; y < N; y++)
Console.Write(sol[x, y] + " ");
Console.WriteLine();
}
}
/* This function solves the
Knight Tour problem using
Backtracking. This function
mainly uses solveKTUtil() to
solve the problem. It returns
false if no complete tour is
possible, otherwise return true
and prints the tour. Please note
that there may be more than one
solutions, this function prints
one of the feasible solutions. */
static bool solveKT()
{
int[,] sol = new int[8, 8];
/* Initialization of
solution matrix */
for (int x = 0; x < N; x++)
for (int y = 0; y < N; y++)
sol[x, y] = -1;
/* xMove[] and yMove[] define
next move of Knight.
xMove[] is for next
value of x coordinate
yMove[] is for next
value of y coordinate */
int[] xMove = {2, 1, -1, -2,
-2, -1, 1, 2};
int[] yMove = {1, 2, 2, 1,
-1, -2, -2, -1};
// Since the Knight is
// initially at the first block
sol[0, 0] = 0;
/* Start from 0,0 and explore
all tours using solveKTUtil() */
if (!solveKTUtil(0, 0, 1, sol,
xMove, yMove))
{
Console.WriteLine("Solution does "+
"not exist");
return false;
}
else
printSolution(sol);
return true;
}
/* A recursive utility function
to solve Knight Tour problem */
static bool solveKTUtil(int x, int y, int movei,
int[,] sol, int[] xMove,
int[] yMove)
{
int k, next_x, next_y;
if (movei == N * N)
return true;
/* Try all next moves from
the current coordinate x, y */
for (k = 0; k < 8; k++)
{
next_x = x + xMove[k];
next_y = y + yMove[k];
if (isSafe(next_x, next_y, sol))
{
sol[next_x,next_y] = movei;
if (solveKTUtil(next_x, next_y, movei +
1, sol, xMove, yMove))
return true;
else
// backtracking
sol[next_x,next_y] = -1;
}
}
return false;
}
// Driver Code
public static void Main()
{
solveKT();
}
}
// This code is contributed by mits.
0 59 38 33 30 17 8 63 37 34 31 60 9 62 29 16 58 1 36 39 32 27 18 7 35 48 41 26 61 10 15 28 42 57 2 49 40 23 6 19 47 50 45 54 25 20 11 14 56 43 52 3 22 13 24 5 51 46 55 44 53 4 21 12
Note that Backtracking is not the best solution for the Knight’s tour problem. See below article for other better solutions. The purpose of this post is to explain Backtracking with an example.
Warnsdorff’s algorithm for Knight’s tour problem
References:
http://see.stanford.edu/materials/icspacs106b/H19-RecBacktrackExamples.pdf
http://www.cis.upenn.edu/~matuszek/cit594-2009/Lectures/35-backtracking.ppt
http://mathworld.wolfram.com/KnightsTour.html
http://en.wikipedia.org/wiki/Knight%27s_tour
