m Coloring Problem
Given an undirected graph and a number m, determine if the graph can be colored with at most m colors such that no two adjacent vertices of the graph are colored with same color. Here coloring of a graph means assignment of colors to all vertices.
Input:
1) A 2D array graph[V][V] where V is the number of vertices in graph and graph[V][V] is adjacency matrix representation of the graph. A value graph[i][j] is 1 if there is a direct edge from i to j, otherwise graph[i][j] is 0.
2) An integer m which is maximum number of colors that can be used.
Output:
An array color[V] that should have numbers from 1 to m. color[i] should represent the color assigned to the ith vertex. The code should also return false if the graph cannot be colored with m colors.
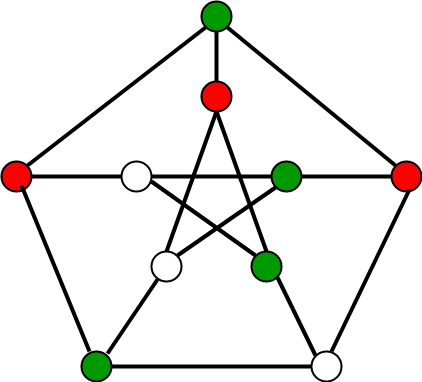
Following is an example of graph that can be colored with 3 different colors.
Naive Algorithm
Generate all possible configurations of colors and print a configuration that satisfies the given constraints.
while there are untried conflagrations
{
generate the next configuration
if no adjacent vertices are colored with same color
{
print this configuration;
}
}
There will be V^m configurations of colors.
Backtracking Algorithm
The idea is to assign colors one by one to different vertices, starting from the vertex 0. Before assigning a color, we check for safety by considering already assigned colors to the adjacent vertices. If we find a color assignment which is safe, we mark the color assignment as part of solution. If we do not a find color due to clashes then we backtrack and return false.
Implementation of Backtracking solution
C/C++
#include<stdio.h>
// Number of vertices in the graph
#define V 4
void printSolution(int color[]);
/* A utility function to check if the current color assignment
is safe for vertex v i.e. checks whether the edge exists or not
(i.e, graph[v][i]==1). If exist then checks whether the color to
be filled in the new vertex(c is sent in the parameter) is already
used by its adjacent vertices(i-->adj vertices) or not (i.e, color[i]==c) */
bool isSafe (int v, bool graph[V][V], int color[], int c)
{
for (int i = 0; i < V; i++)
if (graph[v][i] && c == color[i])
return false;
return true;
}
/* A recursive utility function to solve m coloring problem */
bool graphColoringUtil(bool graph[V][V], int m, int color[], int v)
{
/* base case: If all vertices are assigned a color then
return true */
if (v == V)
return true;
/* Consider this vertex v and try different colors */
for (int c = 1; c <= m; c++)
{
/* Check if assignment of color c to v is fine*/
if (isSafe(v, graph, color, c))
{
color[v] = c;
/* recur to assign colors to rest of the vertices */
if (graphColoringUtil (graph, m, color, v+1) == true)
return true;
/* If assigning color c doesn't lead to a solution
then remove it */
color[v] = 0;
}
}
/* If no color can be assigned to this vertex then return false */
return false;
}
/* This function solves the m Coloring problem using Backtracking.
It mainly uses graphColoringUtil() to solve the problem. It returns
false if the m colors cannot be assigned, otherwise return true and
prints assignments of colors to all vertices. Please note that there
may be more than one solutions, this function prints one of the
feasible solutions.*/
bool graphColoring(bool graph[V][V], int m)
{
// Initialize all color values as 0. This initialization is needed
// correct functioning of isSafe()
int *color = new int[V];
for (int i = 0; i < V; i++)
color[i] = 0;
// Call graphColoringUtil() for vertex 0
if (graphColoringUtil(graph, m, color, 0) == false)
{
printf("Solution does not exist");
return false;
}
// Print the solution
printSolution(color);
return true;
}
/* A utility function to print solution */
void printSolution(int color[])
{
printf("Solution Exists:"
" Following are the assigned colors \n");
for (int i = 0; i < V; i++)
printf(" %d ", color[i]);
printf("\n");
}
// driver program to test above function
int main()
{
/* Create following graph and test whether it is 3 colorable
(3)---(2)
| / |
| / |
| / |
(0)---(1)
*/
bool graph[V][V] = {{0, 1, 1, 1},
{1, 0, 1, 0},
{1, 1, 0, 1},
{1, 0, 1, 0},
};
int m = 3; // Number of colors
graphColoring (graph, m);
return 0;
}
Java
/* Java program for solution of M Coloring problem
using backtracking */
public class mColoringProblem {
final int V = 4;
int color[];
/* A utility function to check if the current
color assignment is safe for vertex v */
boolean isSafe(int v, int graph[][], int color[],
int c)
{
for (int i = 0; i < V; i++)
if (graph[v][i] == 1 && c == color[i])
return false;
return true;
}
/* A recursive utility function to solve m
coloring problem */
boolean graphColoringUtil(int graph[][], int m,
int color[], int v)
{
/* base case: If all vertices are assigned
a color then return true */
if (v == V)
return true;
/* Consider this vertex v and try different
colors */
for (int c = 1; c <= m; c++)
{
/* Check if assignment of color c to v
is fine*/
if (isSafe(v, graph, color, c))
{
color[v] = c;
/* recur to assign colors to rest
of the vertices */
if (graphColoringUtil(graph, m,
color, v + 1))
return true;
/* If assigning color c doesn't lead
to a solution then remove it */
color[v] = 0;
}
}
/* If no color can be assigned to this vertex
then return false */
return false;
}
/* This function solves the m Coloring problem using
Backtracking. It mainly uses graphColoringUtil()
to solve the problem. It returns false if the m
colors cannot be assigned, otherwise return true
and prints assignments of colors to all vertices.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
boolean graphColoring(int graph[][], int m)
{
// Initialize all color values as 0. This
// initialization is needed correct functioning
// of isSafe()
color = new int[V];
for (int i = 0; i < V; i++)
color[i] = 0;
// Call graphColoringUtil() for vertex 0
if (!graphColoringUtil(graph, m, color, 0))
{
System.out.println("Solution does not exist");
return false;
}
// Print the solution
printSolution(color);
return true;
}
/* A utility function to print solution */
void printSolution(int color[])
{
System.out.println("Solution Exists: Following" +
" are the assigned colors");
for (int i = 0; i < V; i++)
System.out.print(" " + color[i] + " ");
System.out.println();
}
// driver program to test above function
public static void main(String args[])
{
mColoringProblem Coloring = new mColoringProblem();
/* Create following graph and test whether it is
3 colorable
(3)---(2)
| / |
| / |
| / |
(0)---(1)
*/
int graph[][] = {{0, 1, 1, 1},
{1, 0, 1, 0},
{1, 1, 0, 1},
{1, 0, 1, 0},
};
int m = 3; // Number of colors
Coloring.graphColoring(graph, m);
}
}
// This code is contributed by Abhishek Shankhadhar
Python
# Python program for solution of M Coloring
# problem using backtracking
class Graph():
def __init__(self, vertices):
self.V = vertices
self.graph = [[0 for column in range(vertices)]\
for row in range(vertices)]
# A utility function to check if the current color assignment
# is safe for vertex v
def isSafe(self, v, colour, c):
for i in range(self.V):
if self.graph[v][i] == 1 and colour[i] == c:
return False
return True
# A recursive utility function to solve m
# coloring problem
def graphColourUtil(self, m, colour, v):
if v == self.V:
return True
for c in range(1, m+1):
if self.isSafe(v, colour, c) == True:
colour[v] = c
if self.graphColourUtil(m, colour, v+1) == True:
return True
colour[v] = 0
def graphColouring(self, m):
colour = [0] * self.V
if self.graphColourUtil(m, colour, 0) == False:
return False
# Print the solution
print "Solution exist and Following are the assigned colours:"
for c in colour:
print c,
return True
# Driver Code
g = Graph(4)
g.graph = [[0,1,1,1], [1,0,1,0], [1,1,0,1], [1,0,1,0]]
m=3
g.graphColouring(m)
# This code is contributed by Divyanshu Mehta
Output:
Solution Exists: Following are the assigned colors 1 2 3 2
References:
http://en.wikipedia.org/wiki/Graph_coloring
