A Time Complexity

A Time Complexity Question

What is the time complexity of following function fun()? Assume that log(x) returns log value in base 2.

void fun()
{
   int i, j;
   for (i=1; i<=n; i++)
      for (j=1; j<=log(i); j++)
         printf("GeeksforGeeks");
}

Time Complexity of the above function can be written as Θ(log 1) + Θ(log 2) + Θ(log 3) + . . . . + Θ(log n) which is Θ (log n!)

Order of growth of ‘log n!’ and ‘n log n’ is same for large values of n, i.e., Θ (log n!) = Θ(n log n). So time complexity of fun() is Θ(n log n).

The expression Θ(log n!) = Θ(n log n) can be easily derived from following Stirling’s approximation (or Stirling’s formula).

      log n! = n log n - n + O(log(n))

Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.

Sources:
http://en.wikipedia.org/wiki/Stirling%27s_approximation

Time Complexity of building a heap

Consider the following algorithm for building a Heap of an input array A.

BUILD-HEAP(A) 
    heapsize := size(A); 
    for i := floor(heapsize/2) downto 1 
        do HEAPIFY(A, i); 
    end for 
END

A quick look over the above algorithm suggests that the running time is $O(nlg(n))$ , since each call to Heapify costs $O(lg(n))$ and Build-Heap makes $O(n)$ such calls.
This upper bound, though correct, is not asymptotically tight.

We can derive a tighter bound by observing that the running time of Heapify depends on the height of the tree ‘h’ (which is equal to lg(n), where n is number of nodes) and the heights of most sub-trees are small.
The height ’h’ increases as we move upwards along the tree. Line-3 of Build-Heap runs a loop from the index of the last internal node (heapsize/2) with height=1, to the index of root(1) with height = lg(n). Hence, Heapify takes different time for each node, which is $O(h)$ .

For finding the Time Complexity of building a heap, we must know the number of nodes having height h.
For this we use the fact that, A heap of size n has at most $\left \lceil \frac{n}{2^{h+1}} \right \rceil$ nodes with height h.

Now to derive the time complexity, we express the total cost of Build-Heap as-

(1) $\begin{flalign*} T(n) &= \sum_{h = 0}^{lg(n)}\left \lceil \frac{n}{2^{h+1}} \right \rceil * O(h)\\ &= O(n * \sum_{h = 0}^{lg(n)}\frac{h}{2^{h}})\\ &= O(n * \sum_{h = 0}^{\infty}\frac{h}{2^{h}})\\ \end{flalign*}$

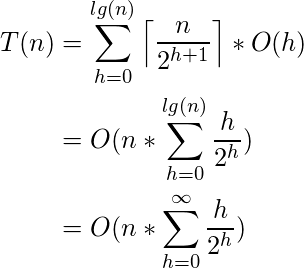
Step 2 uses the properties of the Big-Oh notation to ignore the ceiling function and the constant 2( $2^{h+1} = 2.2^h$ ). Similarly in Step three, the upper limit of the summation can be increased to infinity since we are using Big-Oh notation.

Sum of infinite G.P. (x < 1)

(2) $\begin{align*} \sum_{n = 0}^{\infty}{x}^{n} = \frac{1}{1-x} \end{align*}$

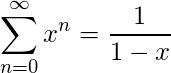
On differentiating both sides and multiplying by x, we get

(3) $\begin{align*} \sum_{n = 0}^{\infty}n{x}^{n} = \frac{x}{(1-x)^{2}} \end{align*}$

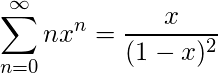
Putting the result obtained in (3) back in our derivation (1), we get

(4) $\begin{flalign*} &= O(n * \frac{\frac{1}{2}}{(1 - \frac{1}{2})^2})\\ &= O(n * 2)\\ &= O(n)\\ \end{flalign*}$

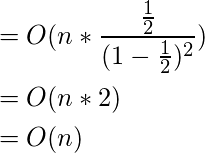
Hence Proved that the Time complexity for Building a Binary Heap is $O(n)$ .

Reference :
http://www.cs.sfu.ca/CourseCentral/307/petra/2009/SLN_2.pdf

Time Complexity where loop variable is incremented by 1, 2, 3, 4 ..

What is the time complexity of below code?

void fun(int n)
{
   int j = 1, i = 0;
   while (i < n)
   {
       // Some O(1) task
       i = i + j;
       j++;
   }
}

The loop variable ‘i’ is incremented by 1, 2, 3, 4, … until i becomes greater than or equal to n.

The value of i is x(x+1)/2 after x iterations. So if loop runs x times, then x(x+1)/2 < n. Therefore time complexity can be written as Θ(√n).

Time Complexity of Loop with Powers

What is the time complexity of below function?

void fun(int n, int k)
{
    for (int i=1; i<=n; i++)
    {
      int p = pow(i, k); 
      for (int j=1; j<=p; j++)
      {
          // Some O(1) work
      }
    }
}

Time complexity of above function can be written as 1^k + 2^k + 3^k + … n1^k.

Let us try few examples:

k=1
Sum = 1 + 2 + 3 ... n 
    = n(n+1)/2 
    = n² + n/2

k=2
Sum = 1² + 2² + 3² + ... n1².
    = n(n+1)(2n+1)/6
    = n³/3 + n²/2 + n/6

k=3
Sum = 1³ + 2³ + 3³ + ... n1³.
    = n²(n+1)²/4
    = n⁴/4 + n³/2 + n²/4

In general, asymptotic value can be written as (n^k+1)/(k+1) + Θ(n^k)

Note that, in asymptotic notations like Θ we can always ignore lower order terms. So the time complexity is Θ(n^k+1/ (k+1))

Performance of loops (A caching question)

Consider below two C language functions to compute sum of elements in a 2D array. Ignoring the compiler optimizations, which of the two is better implementation of sum?

// Function 1
int fun1(int arr[R][C])
{
    int sum = 0;
    for (int i=0; i<R; i++)
      for (int j=0; j<C; j++)
          sum += arr[i][j];
}

// Function 2
int fun2(int arr[R][C])
{
    int sum = 0;
    for (int j=0; j<C; j++)
      for (int i=0; i<R; i++)
          sum += arr[i][j];
}

In C/C++, elements are stored in Row-Major order. So the first implementation has better spatial locality (nearby memory locations are referenced in successive iterations). Therefore, first implementation should always be preferred for iterating multidimensional arrays.

: Scanftree

tutorial

algorithms

analysis-of-algorithms