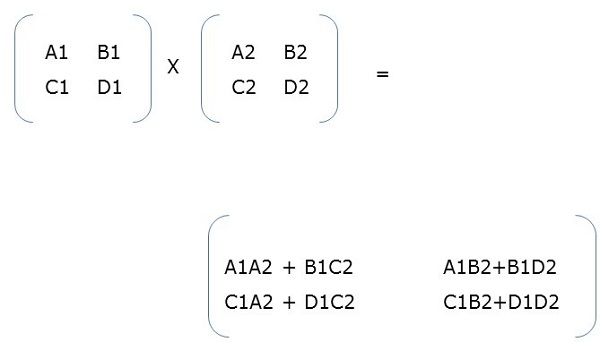
A matrix is a set of numerical and non-numerical data arranged in a fixed number of rows and column. Matrix multiplication is an important multiplication design in parallel computation. Here, we will discuss the implementation of matrix multiplication on various communication networks like mesh and hypercube. Mesh and hypercube have higher network connectivity, so they allow faster algorithm than other networks like ring network.
Mesh Network
A topology where a set of nodes form a p-dimensional grid is called a mesh topology. Here, all the edges are parallel to the grid axis and all the adjacent nodes can communicate among themselves.
Total number of nodes = (number of nodes in row) × (number of nodes in column)
A mesh network can be evaluated using the following factors −
- Diameter
- Bisection width
Diameter − In a mesh network, the longest distance between two nodes is its diameter. A p-dimensional mesh network having kP nodes has a diameter of p(k–1).
Bisection width − Bisection width is the minimum number of edges needed to be removed from a network to divide the mesh network into two halves.
Matrix Multiplication Using Mesh Network
We have considered a 2D mesh network SIMD model having wraparound connections. We will design an algorithm to multiply two n × n arrays using n2 processors in a particular amount of time.
Matrices A and B have elements aij and bij respectively. Processing element PEij represents aij and bij. Arrange the matrices A and B in such a way that every processor has a pair of elements to multiply. The elements of matrix A will move in left direction and the elements of matrix B will move in upward direction. These changes in the position of the elements in matrix A and B present each processing element, PE, a new pair of values to multiply.
Steps in Algorithm
- Stagger two matrices.
- Calculate all products, aik × bkj
- Calculate sums when step 2 is complete.
Algorithm
Procedure MatrixMulti
Begin
for k = 1 to n-1
for all Pij; where i and j ranges from 1 to n
ifi is greater than k then
rotate a in left direction
end if
if j is greater than k then
rotate b in the upward direction
end if
for all Pij ; where i and j lies between 1 and n
compute the product of a and b and store it in c
for k= 1 to n-1 step 1
for all Pi;j where i and j ranges from 1 to n
rotate a in left direction
rotate b in the upward direction
c=c+aXb
End
Hypercube Network
A hypercube is an n-dimensional construct where edges are perpendicular among themselves and are of same length. An n-dimensional hypercube is also known as an n-cube or an n-dimensional cube.
Features of Hypercube with 2k node
- Diameter = k
- Bisection width = 2k–1
- Number of edges = k
Matrix Multiplication using Hypercube Network
General specification of Hypercube networks −
Let N = 2m be the total number of processors. Let the processors be P0, P1…..PN-1.
Let i and ib be two integers, 0 < i,ib < N-1 and its binary representation differ only in position b, 0 < b < k–1.
Let us consider two n × n matrices, matrix A and matrix B.
Step 1 − The elements of matrix A and matrix B are assigned to the n3 processors such that the processor in position i, j, k will have aji and bik.
Step 2 − All the processor in position (i,j,k) computes the product
C(i,j,k) = A(i,j,k) × B(i,j,k)
Step 3 − The sum C(0,j,k) = ΣC(i,j,k) for 0 ≤ i ≤ n-1, where 0 ≤ j, k < n–1.
Block Matrix
Block Matrix or partitioned matrix is a matrix where each element itself represents an individual matrix. These individual sections are known as a block or sub-matrix.
Example
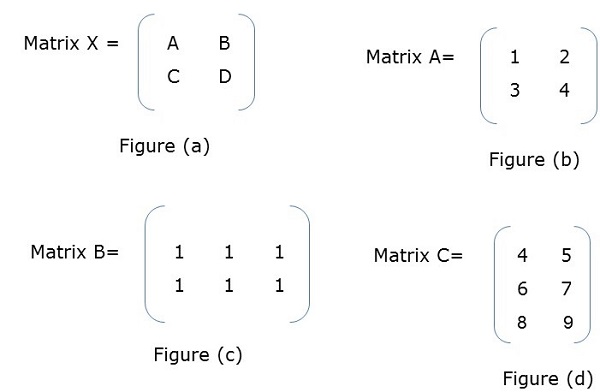
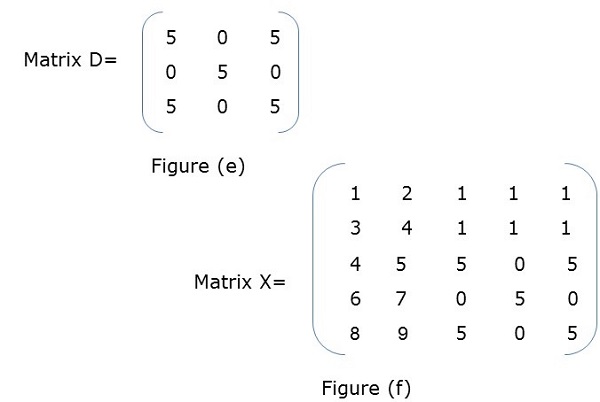
In Figure (a), X is a block matrix where A, B, C, D are matrix themselves. Figure (f) shows the total matrix.
Block Matrix Multiplication
When two block matrices are square matrices, then they are multiplied just the way we perform simple matrix multiplication. For example,