B+ Tree
It is also a type of multi-level indexing. In this tree all the data resides in leaf nodes.
Nowadays b+trees are used in almost every databases.
Block Pointer: These pointers will help to connect with successive blocks (b+ tree children) and the record pointers will connect to the actual data in the memory blocks.
Internal Node Structure
As you can see in the above image that we are having keys and block pointer in internal nodes.Here keys are just to show where to go when traversing to reach leaf nodes.
Lead Node Structure
As you can see in the above image that we are having keys and pointer pairs only in leaf nodes. And one more pointer to point to the next leaf node.<.br> This facilitates faster access while getting data from database.Order in B+ Tree
Let O is order of internal node and Oleaf is order of leaf node.Order of internal Node
Ceil(O/2) to O pointersOrder of Leaf Nodes
Ceil(Oleaf/2) to OleafGate Example 1 on B+ tree
Find order of B+ tree, below are details,(B = Bytes)Search Key = 9 B, Block Size = 512 B, Record Ponter = 7 B, Block Pointer = 6 B
Note: In question they will mention which order but if it’s not given then go for internal node
Formula Internal Node
AnswerOrder * (Block Pointer Size) + (Order - 1) * (Key Size) <= Block Size
Order * 6 + (Order -1 )*9 <= 512
Order = ceil(34.3) = 35 Note: Whenever at least is asked go for ceil of the value and for at max go for floor of value.
Formula Internal Node
Order_of_leaf * (Key Size + Record Pointer Size) + Block Pointer Size <= Block SizeOrder_of_leaf * (9 + 7) + 6 <= 512
Order_of_leaf = ceil(31.2) = 32
Note: Range queries are faster on B+ tree.
Gate Example 2 on B+ tree
In a 4 level B+ tree, if a new node is inserted then how many maximum new nodes can be createdBelow is the image to explain the split
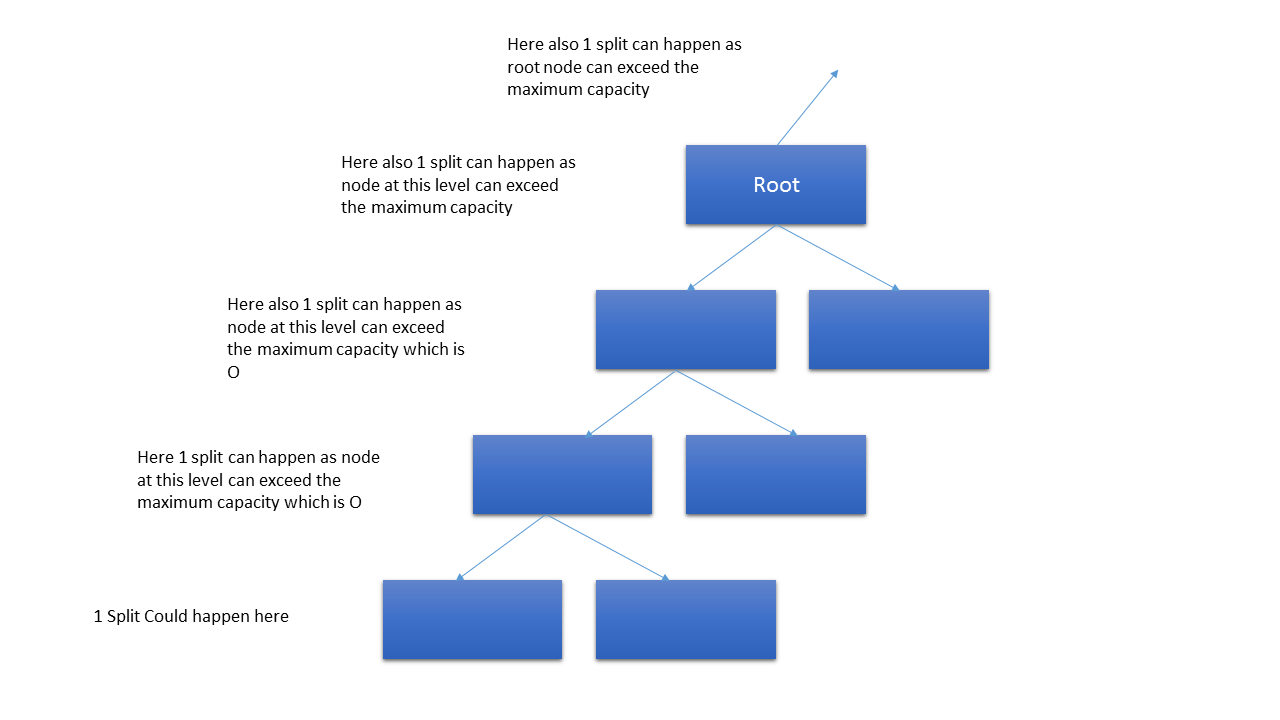 So in total 5 splits will happen.
So in total 5 splits will happen.
