Orthocenter of Triangle, Altitude Calculation
Definition
The point where the altitudes of a triangle meet is known as the Orthocenter. It lies inside for an acute and outside for an obtuse triangle. Altitudes are nothing but the perpendicular line ( AD, BE and CF ) from one side of the triangle ( either AB or BC or CA ) to the opposite vertex. Vertex is a point where two line segments meet ( A, B and C ).
Example
In the below example, o is the Orthocenter.
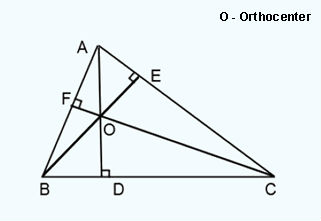
Orthocenter of Triangle
Method to calculate the orthocenter of a triangle
Lets find with the points A(4,3), B(0,5) and C(3,-6).
Step 1
Find the slope of the sides AB, BC and CA using the formula y2-y1/x2-x1. Consider the points of the sides to be x1,y1 and x2,y2 respectively. Kindly note that the slope is represented by the letter 'm'. Slope of AB (m) = 5-3/0-4 = -1/2. Slope of BC (m) = -6-5/3-0 = -11/3. Slope of CA (m) = 3+6/4-3 = 9.
Step 2
Now, lets calculate the slope of the altitudes AD, BE and CF which are perpendicular to BC, CA and AB respectively. The slope of the altitude = -1/slope of the opposite side in triangle. Slope of AD = -1/slope of BC = 3/11. Slope of BE = -1/slope of CA = -1/9. Slope of CF = -1/slope of AB = 2.
Step 3
Once we find the slope of the perpendicular lines, we have to find the equation of the lines AD, BE and CF. Lets find the equation of the line AD with points (4,3) and the slope 3/11. Formula to find the equation of orthocenter of triangle = y-y1 = m(x-x1) y-3 = 3/11(x-4) By solving the above, we get the equation 3x-11y = -21 ---------------------------1 Similarly, we have to find the equation of the lines BE and CF. Equation for the line BE with points (0,5) and slope -1/9 = y-5 = -1/9(x-0) By solving the above, we get the equation x + 9y = 45 -----------------------------2 Equation for the line CF with points (3,-6) and slope 2 = y+6 = 2(x-3) By solving the above, we get the equation 2x - y = 12 ------------------------------3
Step 4
Find the values of x and y by solving any 2 of the above 3 equations. In this example, the values of x any y are (8.05263, 4.10526) which are the coordinates of the Orthocenter(o).
