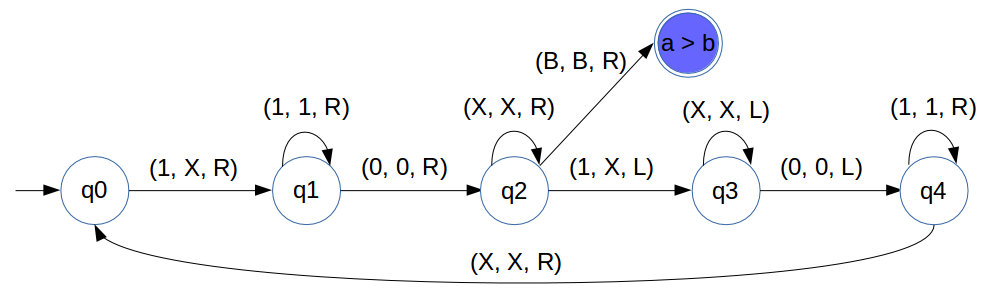
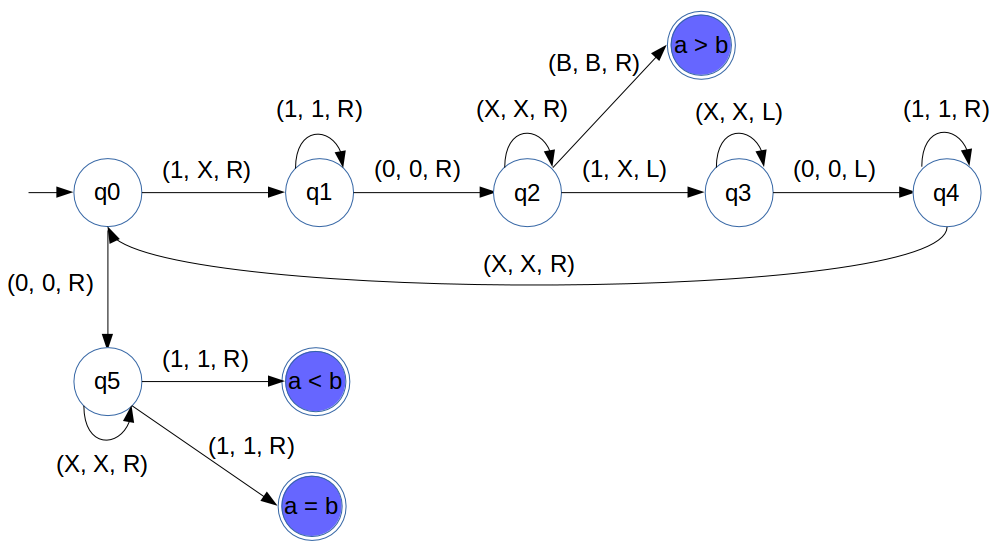
Turing machine as Comparator
Approach for Comparator
- Matching two numbers by comparing '1's
- Example: 11101111 (3 and 4): compare '1's by marking them 'X' and 'Y' respectively
- If '1's are remaining in left of '0' and in right of '0', '1' are finished, then formar is greater
- If '1's are remaining in right of '0' and in left of '0', '1' are finished, then later is greater
- If both '1' are finished then numbers are equal
TAPE movement for string "110111":
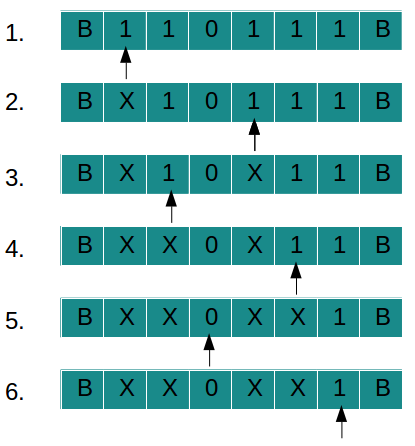
Explanation of TAPE movement
- Input is given as "110111" (2 and 2)
- Scan string from left to right
- Mark '1' as 'X' and then move to right
- Reach right of '0' and mark '1' as 'X' and move left
- Reach 'X' in left of '0' and move one step right
- Again mark '1' as 'X' and then move to right
- Reach right of '0' and pass 'X', mark '1' as 'X' and move left
- Reach 'X' in left of '0'(passing 'Y', '0' and '1')and move one step right
- As '0' is there after 'X' that means all '1's are finished before '0'
- Check for '1' in right of '0'
- Pass '0', 'X' and there is '1' remaining that means second number is greater than first one
- And final state for this will be "a<b"
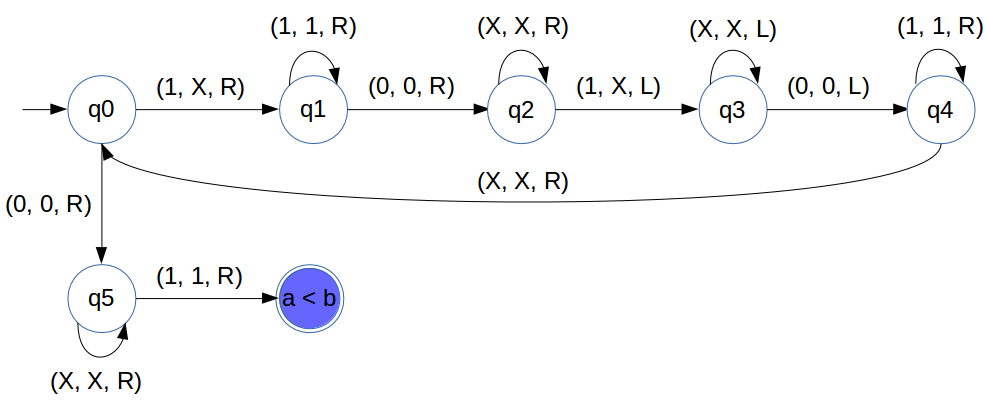
State Transition Diagram
We have designed state transition diagram for adder as follows:
-
Comparator for a = b
- This concept is similar to anbn
- When all '1's are finished in left of '0'
- When all '1's are finished in right of '0'
- Final version of Comparator
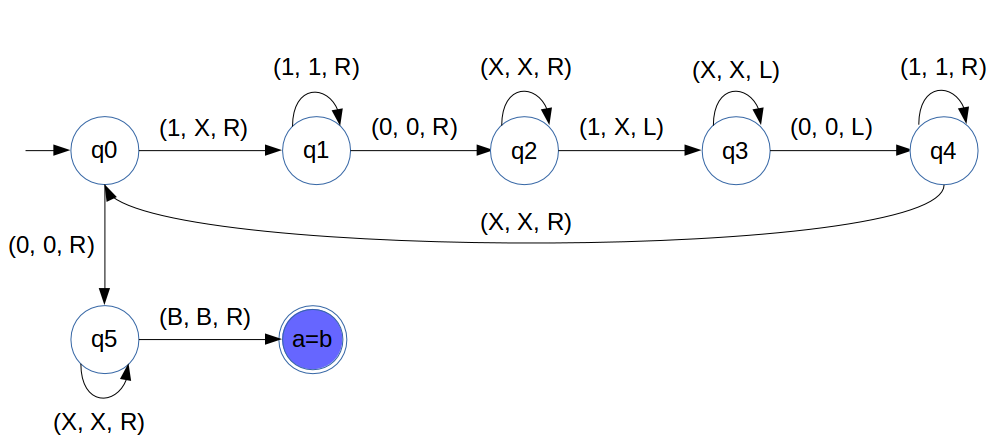
Comparator for a < b
Comparator for a > b