DFA String Examples

---

Create a DFA which accepts strings of odd length

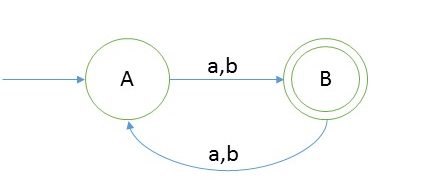
Explanation
As we can see that length of string should be even for that language will be = {a, b, bab, aba, aaa, bbb, baa, aaaaa, bbbbb, ….}
And the language is infinite.

Testing

1. Take a string ‘abbbb’ to test whether it is accepted in the above DFA
2. Scan string from left to right
3. first input we get is a and from start state(A) on ‘a’ we go to B
5. second input is b, from state B on b we will go to start state again.
6. third input is b, from A we go to second state.
7. from second state we go to first state on fourth input symbol b
8. from A on fifth symbol we will go to state B.
9. Now we reached end of string and we are standing on final state.

So we say that string is accepted.

---

Example 2 [Mod n type]

Create a DFA for |w|mod 3 = 0 over w ∈ {a,b}^* So the language,
L = {∈, aaa, bbbb, aab, bbb, ….. }

---

Answer
Here we have a very important observation from above two example that we are having:
Number of states in DFA = total number of possible remainders of given number n, which will be n itself, means there will be n number of states in such examples.
As for number 3, remainders = 0, 1, 2
So number of states in DFA will be 3. And in general this could be applied.
Now let’s create DFA for the above question.

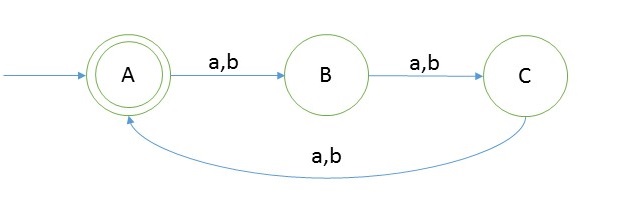
Explanation
As we can see that length of string should be divisible by 3 for that language will be = {∈, abb, bbb, bab, aba, aaa, bbb, baa, aaaaaa, bbbbbb, ….}
And the language is infinite.

---

Testing

1. Take a string ‘ababba’ to test whether it is accepted in the above DFA
2. Scan string from left to right
3. first input we get is a and from start state(A) on ‘a’ we go to B
5. second input is b, from state B on b we will go to state C.
6. third input is a, from C we go to state A.
7. from state C we go to state B on fourth input symbol b
8. from B on fifth symbol we will go to state C.
9. from state C on sixth symbol we will go to state A
10. Now we reached end of string and we are standing on final state.

So we say that string is accepted.
We can also check one negative test: Take one example such as ‘aaaa’, and you will not reach final state. So we say this string is not accepted in the DFA and we can also say that this string does not belong to the given language.

---

We can now make DFA like |w|mod n = m, where n is a number and m is remainder of n.
For example design a DFA such that |w|mod 3 = 1

---

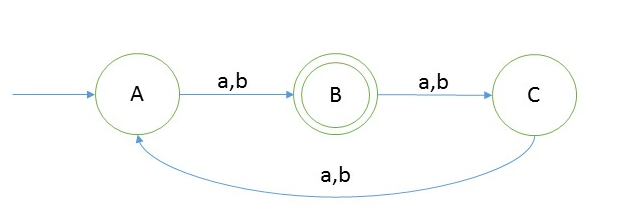
And design a DFA such that |w|mod 3 = 2

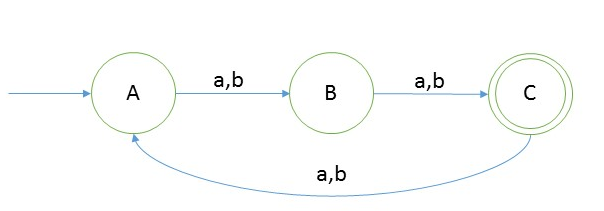
So do you see the trick above, id yes then well done, you got it fella.

---

---