DFA String Examples

Clearly the language is infinite because there is infinite number of strings.
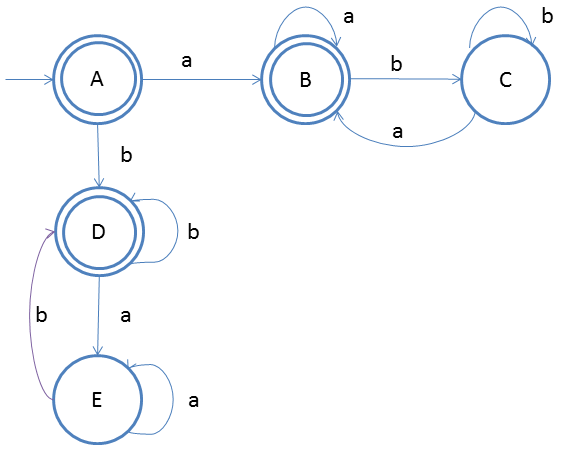This DFA is complement of the previous example.
We will explain complementation in the next section. The idea behind this approach is very simple, follow the steps below and you will understand.

1. We know that if the first input is 'a' then the last input should be 'a', so we start two flows form start state, one for staring with 'a' and another for starting with 'b'
2. Now just design the very basic DFA accepting for ε, that means the start state should final state.
3. In the first flow when 'a' comes form the input string then we should also reach final state as 'a' is also satify the property of DFA
4. After 'a' if any number of 'a' comes then we do not have any problem, that is why a self-loop on state B
6. On state B if b comes then it should be accepted as B is final state so we will create one more state C to get the 'b'
7. On state C if any number of 'b' comes we do not have issues but if 'a' comes then we have to accept it so we will direct input to state B
8. The same mechanism will be for another flow staring from start state A on input 'b'.

Testing 1

1. Lets take one input string aba (this will describe for strings which starts with a and ends with same symbol a)
2. Scan string from left to right
3. First input is a, so from state A we will go to state B
4. Second input is b, so from state B we will go to state C
5. Third input is a, so from state C we will go to state B (final state)

Testing 2

1. Lets take another input string bab(this will describe for strings which starts with b and ends with same symbol b)
2. Scan string from left to right
3. First input is b, so from state A we will go to state D
4. Second input is a, so from state D we will go to state E
5. Third input is b, so from state E we will go to state D(final state)