DFA String Examples
Construct a minimal DFA, which accepts set of all strings over {0, 1}, which when interpreted as binary number is divisible by ‘3’.
Means 110 in binary is equivalent to 6 in decimal and 6 is divisible by 3.
Answer
So if you think in the way of considering remainders if you divide by 3 that is {0, 1, 2}
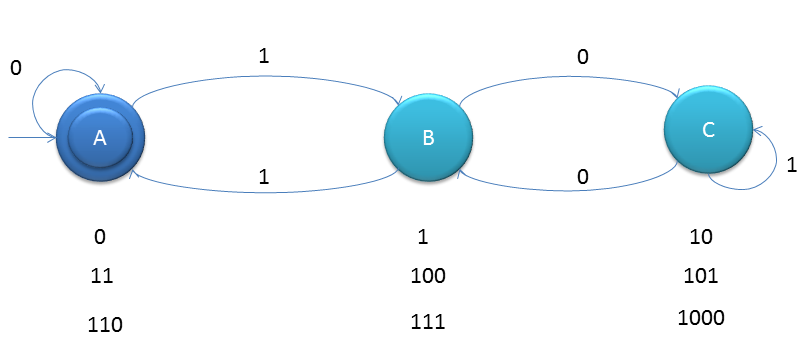
As you can see that binary number which is divisible by 2 is appearing on left state. Short Trick to create such DFAs
Create Transition Table as below
| State | 0 | 1 |
|---|---|---|
| q0 | q0 | q1 |
| q1 | q2 | q0 |
| q2 | q1 | q2 |
- first write the input alphabets, example 0, 1
- there will n states for given number which is divisor.
- start writing states, as for n=3: q0 under 0, q1 under 1
- q2 under 0 and q0 under 1
- q1under 0 and q2 under 1
For ternary pattern and n=4, table will be as follows ;
| State | 0 | 1 | 2 |
|---|---|---|---|
| q0 | q0 | q1 | q2 |
| q1 | q3 | q0 | q1 |
| q2 | q2 | q3 | q0 |
| q3 | q1 | q2 | q3 |
