DFA String Examples

Clearly the language is infinite because there is infinite number of strings.
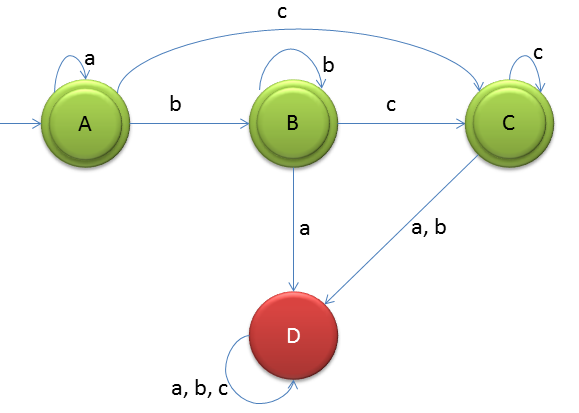The idea behind this approach is very simple, follow the steps below and you will understand.

1. As there is ε we have to make start state as final state.
2. If input is 'a' or multiple number of 'a' then we will loop it to start state itself A
3. If 'b' comes then we will direct it to state B and loop it B state also for any number of 'b'
4. From state B if input 'c' comes then it goes to state C and we will loop on C to accept any number of 'c'
5. Now we will see all the inputs for every state
6. For state A if c comes then yes it valid cause m ≥0. So flow goes to state directly C
7. On state B if 'a' comes then it should get rejected as after 'b' 'a' cannot come. So flow goes to state D(dead state)
8. On state C if 'a'/'b' come then it should get rejected as after 'c' input 'a'/'b' cannot come
9. Like earlier we will loop for 'a', 'b' and 'c' on state D

Testing

1. Lets take one input string aacc
2. Scan string from left to right
3. First input is a, so from state A we will go to state A itself
4. Second input is a, so from state A we will go to state A itself
5. Third input is c, so from state A we will go to state C
6. Fourth input is c, so from state C we will go to state C itself(final state)