DPDA for wcw^R w ε (a,b)^*

Some string will come followed by one 'c', followed by reverse of the string before 'c'.
So we get to know that 'c' will work as an alarm to starting poping STACK.
So we will pop every 'a' with 'a' and every 'b' with 'b'.
For every two a's and b's push them into STACK
When 'c' comes do nothing.
Starting poping STACK: 'a' for 'a' and 'b' for 'b'.
We have designed the PDA for the problem:

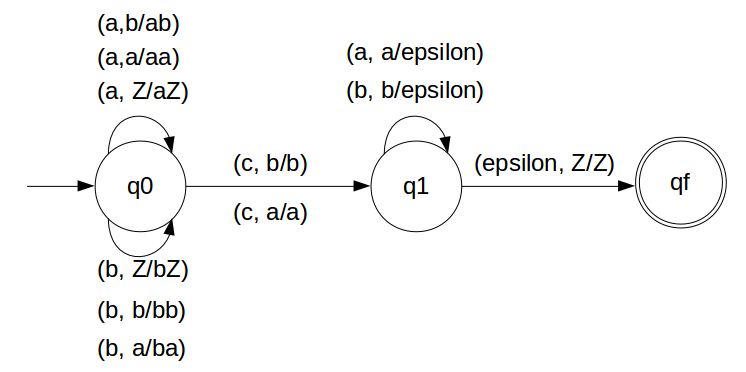
STACK Transiton Function

		δ(q0, a, Z) = (q0, aZ)            
		δ(q0, a, a) = (q0, aa)            
		δ(q0, b, Z) = (q0, bZ)            
		δ(q0, b, b) = (q0, bb)
		δ(q0, a, b) = (q0, ab)            
		δ(q0, b, a) = (q0, ba)            
			
		// this is decision step	
		δ(q0, c, a) = (q1, a)
		δ(q0, c, b) = (q1, b)

		δ(q1, b, b) = (q1, ε)     
		δ(q1, a, a) = (q1, ε)     

		δ(q1, ε, Z) = (qf, Z)     

Note: qf is Final State

---

Explanation

Lets see, how this DPDA is working:
We will take one input string: "abbcbba"

Scan string from left to right

First input is 'a' and follow the rule:

on input 'a' and STACK alphabet Z, push the two 'a's into STACK as : (a,Z/aZ) and state will be q0

Second input is 'b' and so follow the rule:

on input 'b' and STACK alphabet 'a', push the 'b' into STACK as : (b,a/ba) and state will be q0

Third input is 'b' and so follow the rule:

on input 'b' and STACK alphabet 'b', push the 'b' into STACK as : (b,b/bb) and state will be q0

Fourth input is 'c' and so follow the rule:

on input 'c' and STACK alphabet 'a' or 'b' and state q0, do nothing as : (c,b/b) and state will be q1

Fifth input is 'b' and so follow the rule:

on input 'b' and STACK alphabet 'b' (state is q1), pop one 'b' from STACK as : (b,b/ε) and state will be q1

Sixth input is 'b' and so follow the rule:

on input 'b' and STACK alphabet 'b' (state is q1), pop one 'b' from STACK as : (b,b/ε) and state will be q1

Seventh input is 'a' and so follow the rule:

on input 'a' and STACK alphabet 'a' and state q1, pop one 'a' from STACK as : (a,a/ε) and state will remain q1

We reached end of the string, so follow the rule:

on input ε and STACK alphabet Z, go to final state(qf) as : (ε, Z/Z)

---