DPDA for aⁿbⁿc^md^m n,m≥1

Just see the given problem in another perspective.
Number of a's are equal to number of b's
And number of c's are equal to number of d's
That we will achieve by pushing a's and poping a's for every b
And then pushing c's and poping c's for every d's
So in the end of the strings if nothing is left in the STACK then we can say that language is accepted in the PDA.

---

We have designed the PDA for the problem:

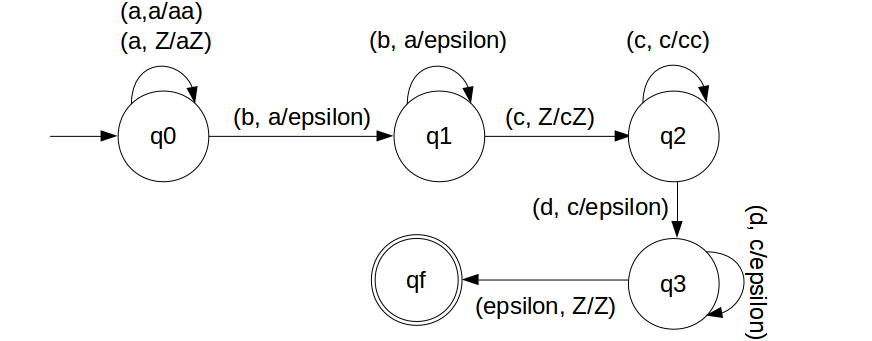
STACK Transiton Function

		δ(q0, a, Z) = (q0, aZ)            
		δ(q0, a, a) = (q0, aa)            
		δ(q0, b, a) = (q1, ε)     
		δ(q1, b, a) = (q1, ε)

		δ(q1, c, Z) = (q2, cZ)             
		δ(q2, c, c) = (q2, cc)             
		δ(q2, d, c) = (q3, ε) 
		δ(q3, d, c) = (q3, ε) 

		δ(q1, ε, Z) = (qf, Z)     

Note: qf is Final State

---

Explanation

Lets see, how this DPDA is working:
We will take one input string: "aabbccdd"

Scan string from left to right

First input is 'a' and follow the rule:

on input 'a' and STACK alphabet Z, push the input 'a' into STACK as : (a,Z/aZ) and state will be q0

Second input is 'a' and so follow the rule:

on input 'a' and STACK alphabet 'a', push the input 'a' into STACK as : (a,a/aa) and state will be q0

Third input is 'b' and so follow the rule:

on input 'b' and STACK alphabet 'a', pop one 'a' from STACK as : (b,a/ε) and state will be q1

Fourth input is 'b' and so follow the rule:

on input 'b' and STACK alphabet 'a' and state q1, pop one 'a' from STACK as : (b,a/ε) and state will remain q1

Fifth input is 'c' and so follow the rule:

on input 'c' and STACK alphabet 'Z' and state is q1, push one 'c' as : (c,Z/cZ) and state will be q2

Sixth input is 'c' and so follow the rule:

on input 'c' and STACK alphabet 'c' and state is q2, push one 'c' as : (c,c/cc) and state will remain q2

Seventh input is 'd' and top of STACK is 'c' so follow the rule:

on input 'd' and STACK alphabet 'c' and state is q2, pop one 'c' as : (d,c/ε) and state will be q3

Eighth input is 'd' and top of STACK is 'c' so follow the rule:

on input 'd' and STACK alphabet 'c' and state is q3, pop one 'c' as : (d,c/ε) and state will be q3

We reached end of the string, so follow the rule:

on input ε and STACK alphabet Z, go to final state(qf) as : (ε, Z/Z)

---

The explanation might be looking over descriptive but please be patient, It will all get clear once you start to get along with the explanation.
So we suggest you to keep doing the practice with the steps mentioned in the explnation