Huffman code

Huffman algorithm is a lossless data compression algorithm. Huffman codes are used for compressing data efficiently from 20% to 90%.
We consider the data to be a sequence of characters.
This algorithm uses a table of the frequencies of occurrence of the characters to build up an optimal way of representing each character as a binary string.

---

Huffman Algorithm

HUFFMAN(C)
1	n ← |C|
2	Q ← C
3	for i 1 to n - 1
4		do allocate a new node z
5			left[z] ← x ← EXTRACT-MIN (Q)
6 			right[z] ← y ← EXTRACT-MIN (Q)
7 			f [z] ← f [x] + f [y]
8 			INSERT(Q, z)
9 	return EXTRACT-MIN(Q)

---

Constructing a Huffman code

Example

Character	Frequency	Fixed-length codeword
a	45	000
b	13	001
c	12	010
d	16	011
e	9	100
f	5	101

There are each character is represented by a unique binary string. If we use a fixed-length code, we need 3 bits to represent the characters.
Total Size = (45+13+12+16+9+5)*10^3
Total Size = 10^5 bits.
Requires bits = 10^5*3 = 3,00,000.

Procedure for Construction of Huffman tree

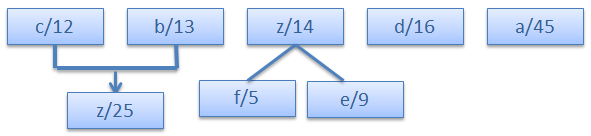
Step 1.
Arrenge the given character in decending order of their frequency.

Step 2.


Step 3.


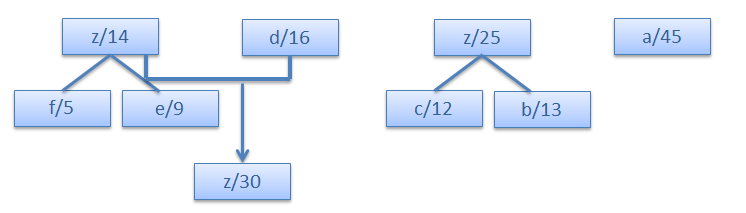
Step 4.


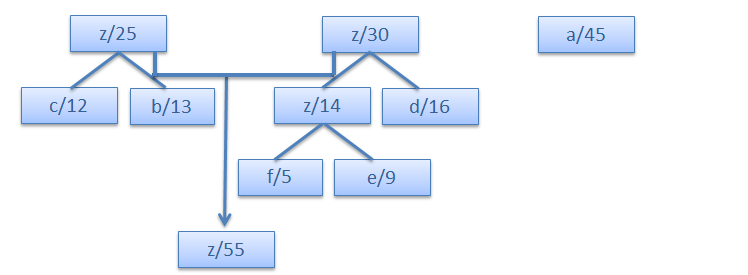
Step 5.


Step 6.


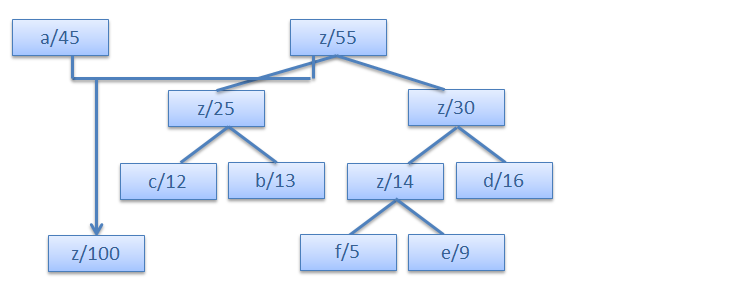
Step 7.

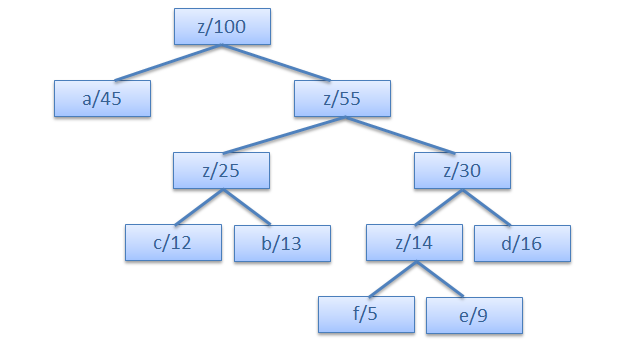
Steps to print codes from Huffman Tree

Traverse huffman tree from the root node. Create an array. While moving to the left child, write 0 to the array. While moving to the right child, write 1 to the array. Print the array when a leaf node is encountered.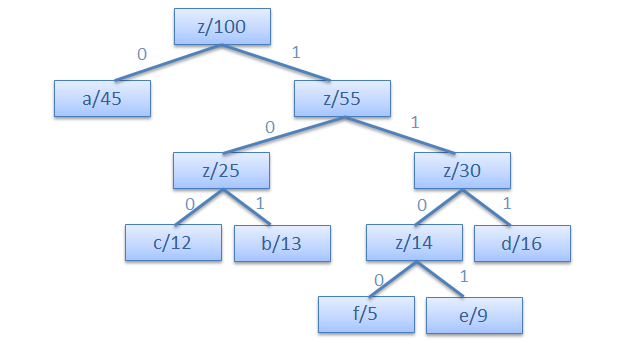

Character	Variable-length codeword	Size of string in bit
a	0	1
b	101	3
c	100	3
d	111	3
e	1101	4
f	1100	4

Calculation for Compression ratio

Size = ((45*1) + (13*3) + (12*3) + (16*3) + (9*4) + (5*4))*10^3)
Requires bits = 224 * 10^3
Requires bits = 224000.
Compression ratio
η = ((3,00,000 - 2,24,000) / 3,00,000)*100
η = 25.33%.

---

Programe For Huffman Code

#include <stdio.h>
#include <stdlib.h>
#include <conio.h>
#define MAX_TREE_HT 100
struct MH_Node
{
	char character;
	unsigned frequency;
	struct MH_Node *l, *r;
};


struct M_Heap
{
	unsigned size;
	unsigned space;
	struct MH_Node **array;
};

struct MH_Node* newNode(char character, unsigned frequency)
{
    struct MH_Node* temp = (struct MH_Node*) malloc(sizeof(struct MH_Node));
    temp->l = temp->r = NULL;
    temp->character = character;
    temp->frequency = frequency;
    return temp;
}


struct M_Heap* createM_Heap(unsigned space)
{
    struct M_Heap* M_Heap = (struct M_Heap*) malloc(sizeof(struct M_Heap));
    M_Heap->size = 0;
    M_Heap->space = space;
    M_Heap->array = (struct MH_Node**)malloc(M_Heap->space * sizeof(struct MH_Node*));
    return M_Heap;
}


void swapMH_Node(struct MH_Node** a, struct MH_Node** b)
{
    struct MH_Node* t = *a;
    *a = *b;
    *b = t;
}


void M_Heapify(struct M_Heap* M_Heap, int idx)
{
    int smallest = idx;
    int l = 2 * idx + 1;
    int r = 2 * idx + 2;

    if (l < M_Heap->size && M_Heap->array[l]->frequency < M_Heap->array[smallest]->frequency)
		smallest = l;

	if (r < M_Heap->size && M_Heap->array[r]->frequency < M_Heap->array[smallest]->frequency)
		smallest = r;

    if (smallest != idx)
    {
		swapMH_Node(&M_Heap->array[smallest], &M_Heap->array[idx]);
		M_Heapify(M_Heap, smallest);
    }
}

int isSizeOne(struct M_Heap* M_Heap)
{
    return (M_Heap->size == 1);
}


struct MH_Node* extractMin(struct M_Heap* M_Heap)
{
    struct MH_Node* temp = M_Heap->array[0];
    M_Heap->array[0] = M_Heap->array[M_Heap->size - 1];
    --M_Heap->size;
    M_Heapify(M_Heap, 0);
    return temp;
}


void insertM_Heap(struct M_Heap* M_Heap, struct MH_Node* MH_Node)
{

    int i = M_Heap->size - 1;
    ++M_Heap->size;
    while (i && MH_Node->frequency < M_Heap->array[(i - 1)/2]->frequency)
    {
		M_Heap->array[i] = M_Heap->array[(i - 1)/2];
		i = (i - 1)/2;
    }
    M_Heap->array[i] = MH_Node;
}


void buildM_Heap(struct M_Heap* M_Heap)
{
    int n = M_Heap->size - 1;
    int i;
    for (i = (n - 1) / 2; i >= 0; --i)
		M_Heapify(M_Heap, i);
}


void printArr(int arr[], int n)
{
    int i;
    for (i = 0; i < n; ++i)
		printf("%d", arr[i]);
		printf("\n");
}


int isLeaf(struct MH_Node* root)
{
    return !(root->l) && !(root->r) ;
}


struct M_Heap* createAndBuildM_Heap(char character[], int frequency[], int size)
{
	int i;
    struct M_Heap* M_Heap = createM_Heap(size);
    for (i = 0; i < size; ++i)
        M_Heap->array[i] = newNode(character[i], frequency[i]);
    M_Heap->size = size;
    buildM_Heap(M_Heap);
    return M_Heap;
}
 

struct MH_Node* buildHuffmanTree(char character[], int frequency[], int size)
{
    struct MH_Node *l, *r, *top;
    struct M_Heap* M_Heap = createAndBuildM_Heap(character, frequency, size);

    while (!isSizeOne(M_Heap))
    {
        l = extractMin(M_Heap);
        r = extractMin(M_Heap);
        top = newNode('$', l->frequency + r->frequency);
        top->l = l;
        top->r = r;
        insertM_Heap(M_Heap, top);
    }
    return extractMin(M_Heap);
}
 
void printCodes(struct MH_Node* root, int arr[], int top)
{
    if (root->l)
    {
        arr[top] = 0;
        printCodes(root->l, arr, top + 1);
    }
 
    if (root->r)
    {
        arr[top] = 1;
        printCodes(root->r, arr, top + 1);
    }
 
    if (isLeaf(root))
    {
        printf("%c: ", root->character);
        printArr(arr, top);
    }
}
 
void HuffmanCodes(char character[], int frequency[], int size)
{
	struct MH_Node* root = buildHuffmanTree(character, frequency, size);
	int arr[MAX_TREE_HT], top = 0;
	printCodes(root, arr, top);
}

void main()
{
	char arr[] = {'a', 'b', 'c', 'd', 'e', 'f'};
	int frequency[] = {5, 9, 12, 13, 16, 45};
	int size; 
	clrscr();
	size = sizeof(arr)/sizeof(arr[0]);
	HuffmanCodes(arr, frequency, size);
	getch();
}