Counting sort

Counting sort is a linear time sorting algorithm used to sort items when they belong to a fixed and finite set. Integers which lie in a fixed interval, say k1 to k2, are examples of such items.

Algorithm

COUNTING-SORT(A,B,k)

1. let C[0..k] be a new array

2. for i = 0 to k

3. 		C[i] = 0

4. for j = 1 to A.length

5. 		C[A[j]] = C[A[j]] + 1

6. // C[i] now contains the number of elements equal to i .

7. for i = 1 to k

8. 		C[i] = C[i] + C[i - 1]

9. // C[i] now contains the number of elements less than or equal to i .

10.for j = A.length downto 1

11.		B[C[A[j]]] = A[j]

12.		C[A[j]] = C[A[j]] - 1

Counting sort Implementation

#include <stdio.h>

#include <conio.h>

void Counting_sort(int [], int, int);

void main()

{

	int n,i,k=0,A[15];

	clrscr();

	printf("\n\n

	\t\t\t----------Counting Sort----------\n\n\n");

	printf("Enter the number of input : ");

	scanf("%d",&n);

	printf("\nEnter the elements to be sorted :\n");

	for (i=1;i<=n;i++)

	{

		scanf("%d",&A[i]);

		if(A[i] > k)

		{

			k = A[i];

		}

	}

	Counting_sort(A, k, n);

	getch();

}



void Counting_sort(int A[], int k, int n)

{

	int i, j;

	int B[15], C[100];

	for(i = 0; i <= k; i++)

		C[i] = 0;

	for(j =1; j <= n; j++)

		C[A[j]] = C[A[j]] + 1;

	for(i = 1; i <= k; i++)

		C[i] = C[i] + C[i-1];

	for(j = n; j >= 1; j--)

	{

		B[C[A[j]]] = A[j];

		C[A[j]] = C[A[j]] - 1;

	}

	printf("\t\t\t----Sorted Array Using Counting Sort----\n\n\n" );

	printf("\nThe Sorted array is : ");

	for(i=1;i<=n;i++)

	{

		printf("\t");

		printf("%d",B[i]);



	}

}

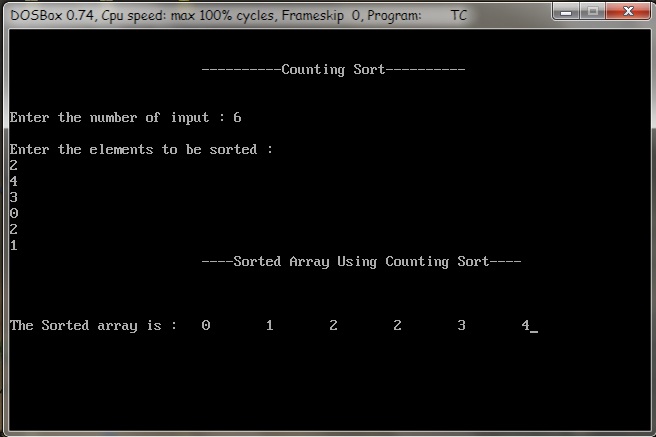
Output