Deletion in B-Tree

For deletion in b tree we wish to remove from a leaf. There are three possible case for deletion in b tree.
Let k be the key to be deleted, x the node containing the key. Then the cases are:

Case-I

If the key is already in a leaf node, and removing it doesn’t cause that leaf node to have too few keys, then simply remove the key to be deleted. key k is in node x and x is a leaf, simply delete k from x.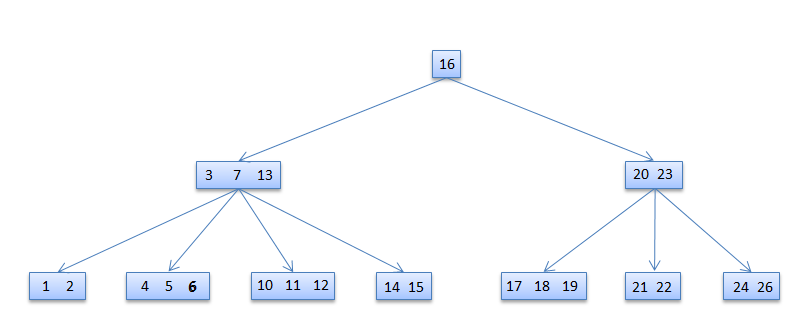
6 deleted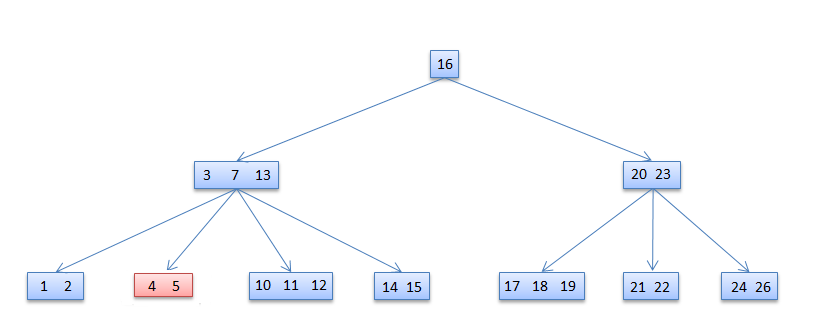

---

Case-II

If key k is in node x and x is an internal node, there are three cases to consider:

Case-II-a

If the child y that precedes k in node x has at least t keys (more than the minimum), then find the predecessor key k' in the subtree rooted at y. Recursively delete k' and replace k with k' in x

---

Case-II-b

Symmetrically, if the child z that follows k in node x has at least t keys, find the successor k' and delete and replace as before. Note that finding k' and deleting it can be performed in a single downward pass.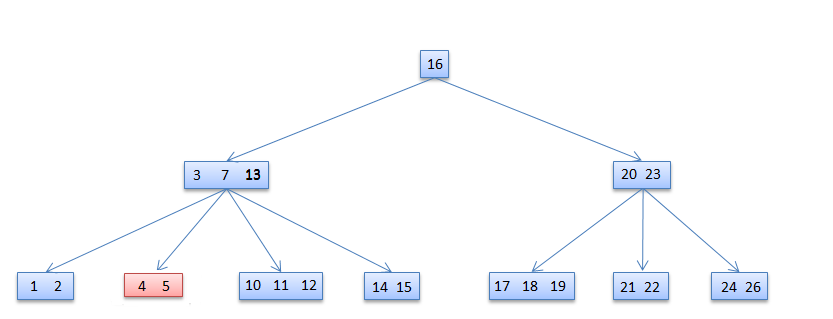

13 deleted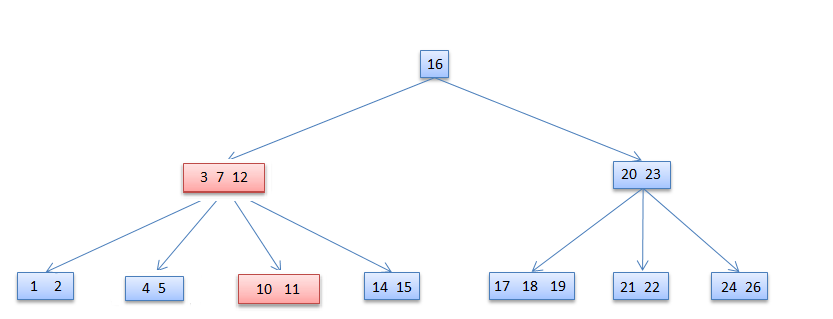

---

Case-II-c

Otherwise, if both y and z have only t−1 (minimum number) keys, merge k and all of z into y, so that both k and the pointer to z are removed from x. y now contains 2t − 1 keys, and subsequently k is deleted.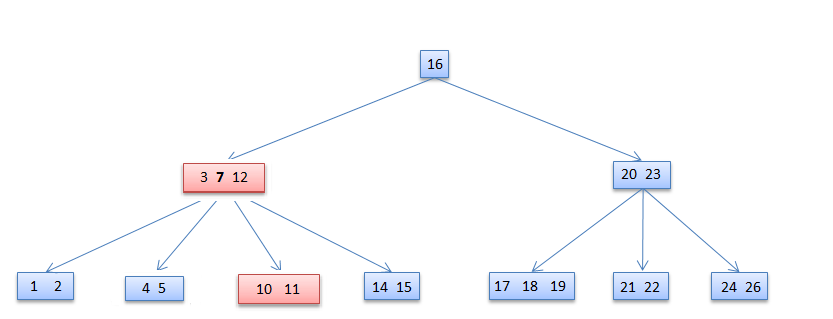


7 deleted

---

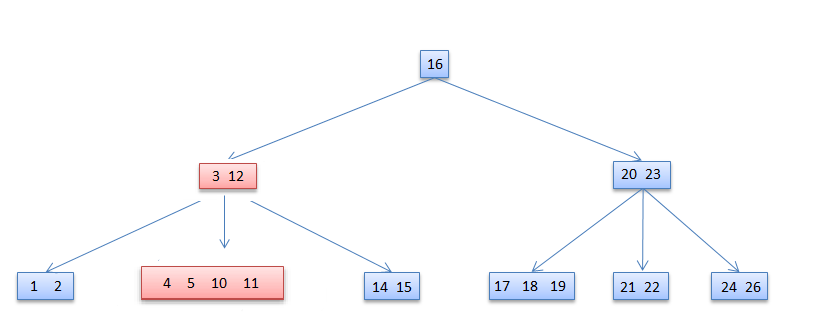
Case-III

If key k is not present in an internal node x, determine the root of the appropriate subtree that must contain k. If the root has only t − 1 keys, execute either of the following two cases to ensure that we descend to a node containing at least t keys. Finally, recurse to the appropriate child of x.

Case-III-a

If the root has only t−1 keys but has a sibling with t keys, give the root an extra key by moving a key from x to the root, moving a key from the roots immediate left or right sibling up into x, and moving the appropriate child from the sibling to x.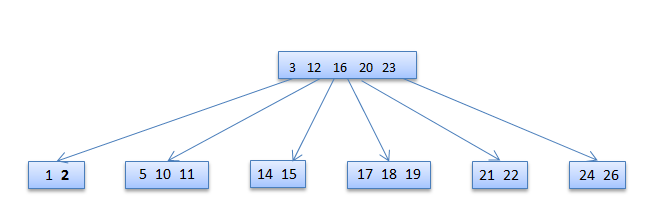


2 deleted

---

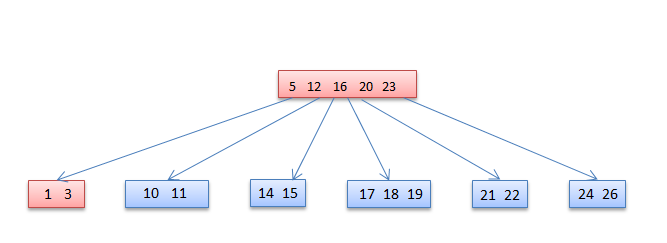
Case-III-b

If the root and all of its siblings have t−1 keys, merge the root with one sibling. This involves moving a key down from x into the new merged node to become the median key for that node.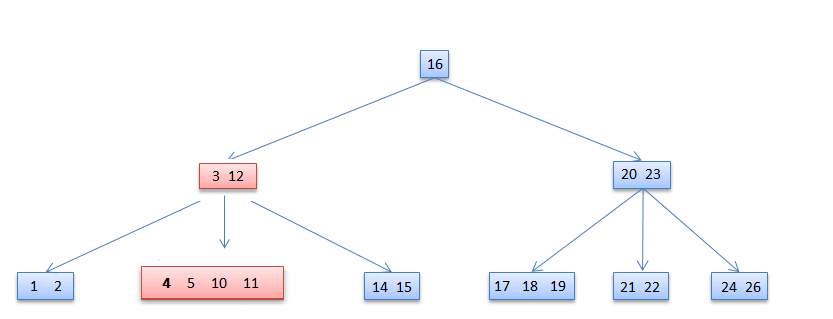


4 deleted

---

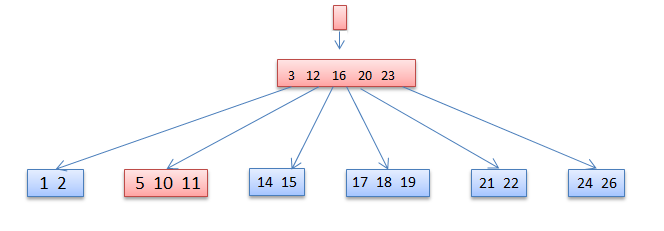
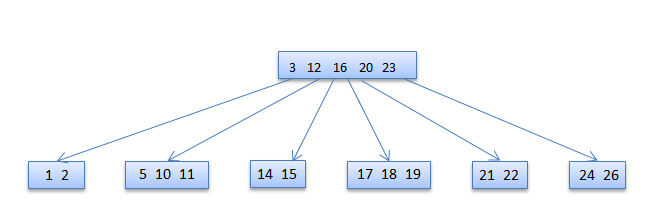
Algorithm For deletion in b tree

1. B-Tree-Delete-Key(x, k)

2. 	if not leaf[x] then

3.		y ← Preceding-Child(x)

4.		z ← Successor-Child(x)

5.		if n[y] > t − 1 then

6.			k' ← Find-Predecessor-Key(k, x)

7.			Move-Key(k', y, x)

8.			Move-Key(k, x, z)

9.			B-Tree-Delete-Key(k, z)

10.		else if n[z] > t − 1 then

11.			k' ← Find-Successor-Key(k, x)

12.			Move-Key(k', z, x)

13.			Move-Key(k, x, y)

14.			B-Tree-Delete-Key(k, y)

15.		else

16.			Move-Key(k, x, y)

17.			Merge-Nodes(y, z)

18.			B-Tree-Delete-Key(k, y)

19.		else (leaf node)

20.		 y ← Preceding-Child(x)

21.		 z ← Successor-Child(x)

22.		 w ← root(x)

23.		 v ← RootKey(x)

24.			if n[x] > t − 1 then Remove-Key(k, x)

25.			else if n[y] > t − 1 then

26.				k' ← Find-Predecessor-Key(w, v)

27.				Move-Key(k', y,w)

28.				k' ← Find-Successor-Key(w, v)

29.				Move-Key(k',w, x)

30.				B-Tree-Delete-Key(k, x)

31.			else if n[w] > t − 1 then

32.				k' ← Find-Successor-Key(w, v)

33.				Move-Key(k', z,w)

34.				k' ← Find-Predecessor-Key(w, v)

35.				Move-Key(k',w, x)

36.				B-Tree-Delete-Key(k, x)

37.			else

38.				s ← Find-Sibling(w)

39.				w' ← root(w)

40.					if n[w'] = t − 1 then

41.						Merge-Nodes(w',w)

42.						Merge-Nodes(w, s)

43.						B-Tree-Delete-Key(k, x)

44.					else

45.						Move-Key(v,w, x)

46.						B-Tree-Delete-Key(k, x)