An activity selection problem

The activity selection problem is a mathematical optimization problem. That concerning the selection of non-conflicting activities. Each activity assigned by a start time (si) and finish time (fi). The activity selection problem is to select the maximum number of activities that can be performed by a single machine, assuming that a machine can only work on a single activity at a time.

---

GREEDY ACTIVITY SELECTOR Algorithm

GREEDY-ACTIVITY-SELECTOR(s, f)

1.  n ← length[s]
2.  A ← {a1}
3.  i ← 1
4.  for m ← 2 to n
5.  	do if sm ≥ fi
6.  	then A ← A U {am}
7.  	i ← m
8.  return A

---

Example

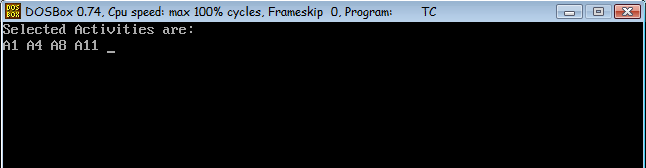
Start time (si)	finish time (fi)	Activity name
1	4	A1
3	5	A2
0	6	A3
5	7	A4
3	9	A5
5	9	A6
6	10	A7
8	11	A8
8	12	A9
2	14	A10
12	16	A11

Selected Activities are: A1, A4, A8, A11

---

activity selection problem in c

#include<stdio.h>

#include<conio.h>



void activities(int s[], int f[], int n)

{

	int i, j;

	printf ("Selected Activities are:\n");

	i = 1;

	printf("A%d ", i);

	for (j = 1; j < n; j++)

	{

		if (s[j] >= f[i])

		{

			printf ("A%d ", j+1);

			i = j;

		}

	}

}



void main()

{

	int s[] =  {1, 3, 0, 5, 3, 5, 6, 8, 8, 2, 12};

	int f[] =  {4, 5, 6, 7, 9, 9, 10, 11, 12, 14, 16};

	int n = sizeof(s)/sizeof(s[0]);

	clrscr();

	activities(s, f, n);

	getchar();

	getch();

}

Output