Bellman-ford Algorithm

Bellman–Ford algorithm is an algorithm that solves the shortest path from a single source vertex to all of the other vertices in a weighted digraph.

Bellman-Ford algorithm returns a boolean value indicating whether or not there is a negative-weight cycle that is reachable from the source. If there is such a cycle, the algorithm indicates that no solution exists. If there is no such cycle, the algorithm produces the shortest paths and their weights.

This algorithm returns TRUE if and only if the graph contains no negativeweight cycles that are reachable from the source.

---

Bellman-ford Algorithm

BELLMAN-FORD(G, w, s)
1 INITIALIZE-SINGLE-SOURCE(G, s)
2 for i ← 1 to |V[G]| - 1
3 	do for each edge (u, v)  E[G]
4 		do RELAX(u, v, w)
5 for each edge (u, v)  E[G]
6 	do if d[v] > d[u] + w(u, v)
7 		then return FALSE
8 return TRUE

---

Example

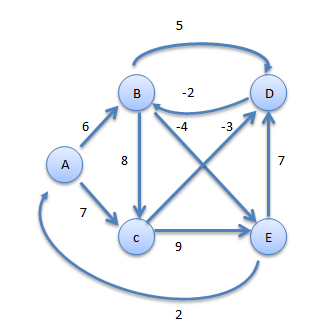
Procedure for Bellman-ford Algorithm

Step1

Consider A as source vertex

No. of Nodes        A        B        C        D        E Distance        0        6        7        ∞        ∞ Distance From       A        A        A

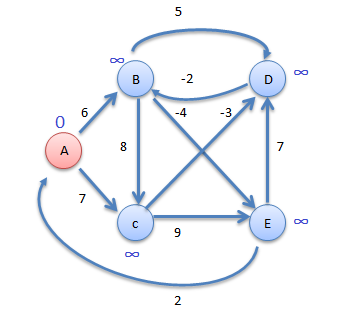
Step2

Now consider vertex B

No. of Nodes        A        B        C        D        E Distance        0        6        7        11        2 Distance From        A        A       A        B        B

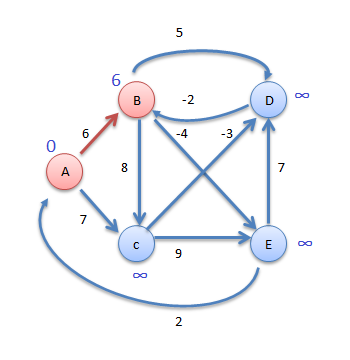
Step3

Now consider vertex E

No. of Nodes        A        B        C        D        E Distance        0        6        7        9        2 Distance From        A        A        A        E       B

Step4

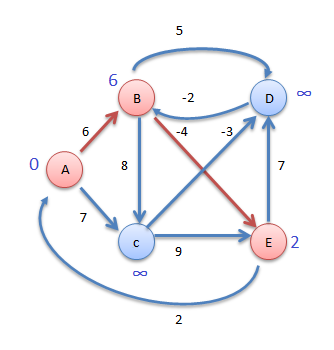
Now consider vertex C

No. of Nodes        A        B        C        D        E Distance        0        6       7        4        2 Distance From       A        A       A        C        B

Step5

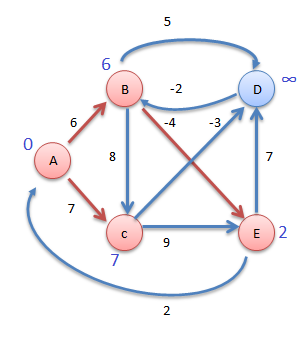
Now consider vertex D

No. of Nodes        A       B        C        D        E Distance        0        2       7        4        2 Distance From        A        D       A        C       B

Step6

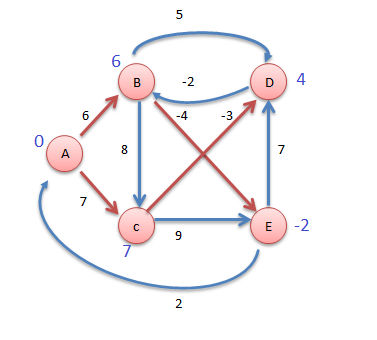
Now consider vertex B

No. of Nodes        A       B        C        D        E Distance        0        2       7       4       -2 Distance From        A       D       A        C        B

Step7

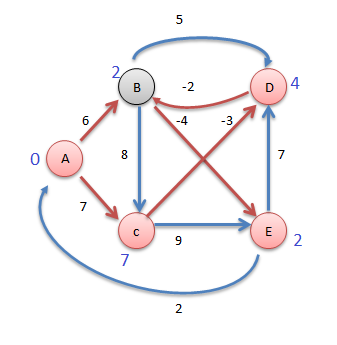
Now consider vertex E

No. of Nodes        A       B        C        D        E Distance       0        2        7        4       -2 Distance From        A        D       A        C        B

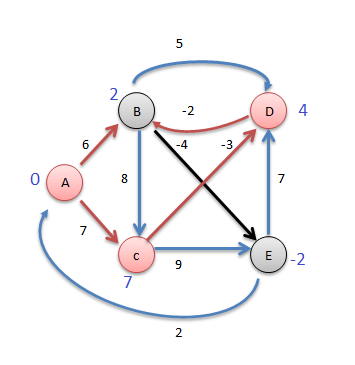
Vertex	Distance from A
A	0
B	2
C	7
D	4
E	-2

---