The edge-connectivity λ(G) of a connected graph G is the smallest number of edges whose removal disconnects G. When λ(G) ≥ k, the graph G is said to be k-edge-connected.
For example, the edge connectivity of the below four graphs G1, G2, G3, and G4 are as follows:
- G1 has edge-connectivity 1.
- G2 has edge connectivity 1.
- G3 has edge connectivity 2.
- G4 has edge connectivity 2.
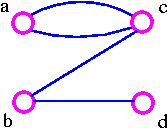
The above graph G1 can be split up into two components by removing one of the edges bc or bd. Therefore, edge bc or bd is a bridge.
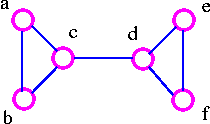
The above graph G2 can be disconnected by removing a single edge, cd. Therefore, edge cd is a bridge.
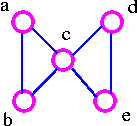
The above graph G3 cannot be disconnected by removing a single edge, but the removal of two edges (such as ac and bc) disconnects it.
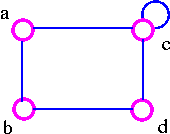
The above graph G4 can be disconnected by removing two edges such as ac and dc.
