Euler Graphs
Consider the following road map
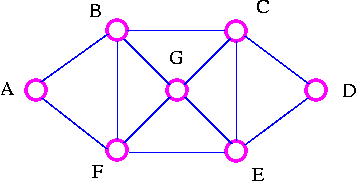
The explorer's Problem: An explorer wants to explore all the routes between a number of cities. Can a tour be found which traverses each route only once? Particularly, find a tour which starts at A, goes along each road exactly once, and ends back at A.
Examples of such tour are
| A | B | C | D | E | F | B | G | C | E | G | F | A | ||
| A | F | G | C | D | E | G | B | C | E | F | B | A |
The Explorer travels along each road (edges) just once but may visit a particular city (vertex) several times.
The Traveler's Problem
A traveler wants to visit a number of cities. Can a tour be found which visits each city only once? Particularly, find a tour which starts at A, goes to each city exactly once, and ends back at A.
Examples of such tour are
| A | B | C | D | E | G | F | A | ||
| A | F | E | D | C | G | B | A |
The travelers visits each city (vertex) just once but may omit several of the roads (edges) on the way.
Eulerian Trail
A connected graph G is Eulerian if there is a closed trail which includes every edge of G, such a trail is called an Eulerian trail.
Hamiltonian Cycle
A connected graph G is Hamiltonian if there is a cycle which includes every vertex of G; such a cycle is called a Hamiltonian cycle.
Consider the following examples:
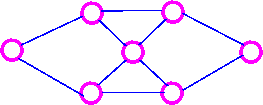
This graph is BOTH Eulerian and
Hamiltonian.
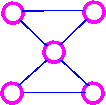
This graph is Eulerian, but NOT
Hamiltonian.
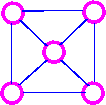
This graph is an Hamiltionian, but NOT Eulerian.
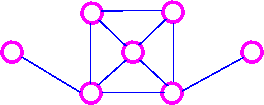
This graph is NEITHER Eulerian
NOR Hamiltionian
Theorem Let G be a connected graph. Then G is Eulerian if and only if every vertex of G has even degree.
-
Necessary Condition
- If G is Eulerian, then every vertex of G has even degree.
-
Sufficient Condition
- If every vertex of G has even degree, then G is Eulerian.
Eulerian-Type Problems
- Edge-traceable graphs.
- Diagrams-Tracing Puzzles.
- Dominoes.
- Mazes and labyrinths,
- The Chinese Postman Problem.
- The Rotating Drum Problem.
Neither necessary nor sufficient condition is known for a graph to be Hamiltonian. The search for necessary or sufficient conditions is a major area of study in graph theory today.
Sufficient Condition
Dirac's Theorem Let G be a simple graph with n vertices where n ≥ 3 If deg(v) ≥ 1/2 n for each vertex v, then G is Hamiltonian.
For example,
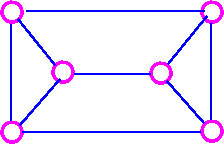
n = 6 and deg(v) = 3 for each vertex, so this graph is Hamiltonian by Dirac's theorem.
Ore's Theorem Let G be a simple graph with n vertices where n ≥ 2 if deg(v) + deg(w) ≥ n for each pair of non-adjacent vertices v and w, then G is Hamiltonian.
For example,
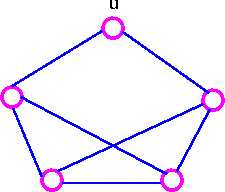
n = 5 but deg(u) = 2, so Dirac's theorem does not apply. However, deg(v) + deg(w) ≥ 5 for all pairs of vertices v and w (infact, for all pairs of vertices v and w), so this graph is Hamiltonian by Ore's theorem.
Note that if deg(v) ≥ 1/2 n for each vertex, then deg(v) + deg(w) ≥ n for each pair of vertices v and w. It follows that Dirac's theorem can be deduced from Ore's theorem, so we prove only Ore's threoem.
Hamiltonain - Type Problem
- Gray Codes.
- The Traveling Salesperson Problem
- Ranking in Tournaments.
