Vertex Connectivity
The connectivity (or vertex connectivity) K(G) of a connected graph G (other than a complete graph) is the minimum number of vertices whose removal disconnects G. When K(G) ≥ k, the graph is said to be k-connected (or k-vertex connected). When we remove a vertex, we must also remove the edges incident to it. As an example consider following graphs.
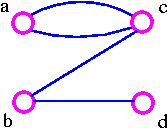
The above graph G can be disconnected by removal of single vertex (either b or c). The G has connectivity 1.
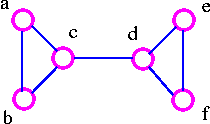
The above graph G can be disconnected by removal of single vertex (either c or d). The vertex c or d is a cut-vertex. The G has connectivity 1.
g46.gif
The above G can be disconnected by removing just one vertex i.e., vertex c. The vertex c is the cut-vertex. The G has connectivity 1.
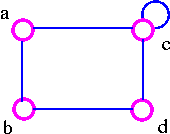
The above G cannot be disconnected by removing a single vertex, but the removal of two non-adjacent vertices (such as b and c) disconnects it. The G has connectivity 2.
