Graph Coloring
Vertex Coloring
Let G be a graph with no loops. A k-coloring of G is an assignment of k colors to the vertices of G in such a way that adjacent vertices are assigned different colors. If G has a k-coloring, then G is said to be k-coloring, then G is said to be k-colorable. The chromatic number of G, denoted by X(G), is the smallest number k for which is k-colorable. For example,
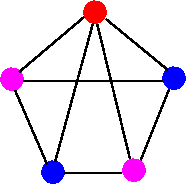
3-coloring
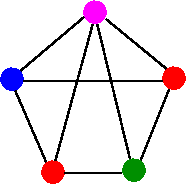
4-coloring
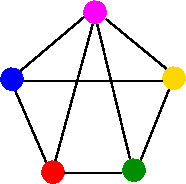
5-coloring
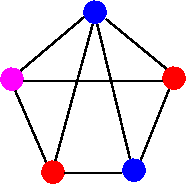
Not a permissible coloring, since one of the edge has color blue at both ends.
It is easy to see from above examples that chromatic number of G is at least 3. That is X(G) ≤ 3, since G has a 3-coloring in first diagram. On the other hand, X(G) ≥ 3, since G contains three mutually adjacent vertices (forming a triangle)., which must be assigned different colors. Therefore, we have X(G) = 3.
Lower Bound of X(G)
To obtain a lower bound for X(G), we look for the largest complete subgraph in G. For example, consider the following graph.
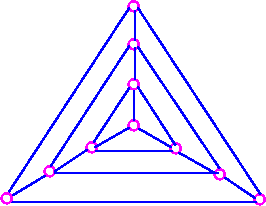
Since this graph contains the complete graph K4, therefore X(G) ≥ 4.
Upper Bound of X(G)
To obtain an upper bound for X(G), we note that if G has n vertices, then X(G) ≤ 4. However, this upper bound is very poor and we can improve it if we know the largest vertex-degree in G, which gives us the following theorem.
Theorem 1 If G is a simple graph whose maximum vertex-degree is d, then X(G) ≤ d+1.
Proof Idea Mathematical induction on the number of vertices of G.
We can prove the following slightly stronger theorem, which illustrates the same idea.
Brook's Theorem 2 Let G be a connected simple graph whose maximum vertex-degree is d. If G is neither a cycle graph with an odd number of vertices, nor a complete graph, then X(G) ≤ d.
To illustrate the use of Brook's theorem, consider graph G.

Since G contains the complete graph K4, so X(G) ≤ 4. On the other hand, G satisfies the conditions of Brook's theorem with d=4 and so X(G) ≤ 4. It follows from these two pieces of information that X(G) = 4.
It is important to note that Brook's theorem does not always give a tight bound. For example, if G is the bipartite graph k1,100, then X(G) = 2, whereas Brook's theorem gives us the upper bound X(G) ≤ 100.
Chromatic Polynomials
All known algorithms for finding the chromatic number of a graph are some what inefficient. A good estimation for the chromatic number of given graph involves the idea of a chromatic polynomials.
Let G be a simple graph, and let PG(k) be the number of ways of coloring the vertices of G with k colors in such a way that no two adjacent vertices are assigned the same color. The function PG(k) is called the chromatic polynomial of G.
As an example, consider complete graph K3 as shown in the following figure.
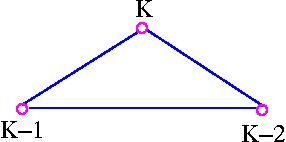
Then the top vertex can be assigned any of the k colors, the left vertex can be assigned any k-1 colors, and right vertex can be assigned any of the k-2 colors. The chromatic polynomial of K3 is therefore k(k-1)(k-2). The extension of this immediately gives us the following result.
If G is the complete graph Kn, then PG(k) = k(k - 1)(k - 2) . . . (k - n +1).
Edge Colorings
Let G be a graph with no loops. A k-edge-coloring of G is an assignment of k colors to the edges of G in such a way that any two edges meeting at a common vertex are assigned different colors,. If G has a k-edge coloring, then G is said to be k-edge colorable. The chromatic index of G, denoted by X`(G), is the smallest k for which G is k-edge-colorable. For example, consider the following graphs with eight edges:
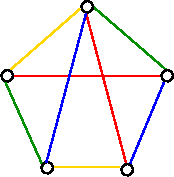
4-edges-coloring
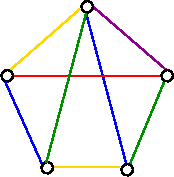
5-edge-coloring
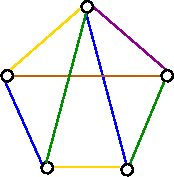
6-edge-coloring
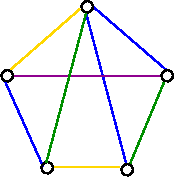
Not a permissible coloring. Since two of the edges colored blue meet at a common vertex
From the above examples, it follows that X`(G) ≤ 4, since G has a 4-edge-coloring in figure a (above). On the other hand, X`(G) ≥ 4, since G contains 4 edges meeting at a common vertex i.e., a vertex of degree 4, which must be assigned different colors. Therefore, X`(G) = 4.
Lower Bound of X`(G)
To obtain a lower bound for X`(G), we look for the largest vertex-degree, d, in given G, which gives us X`(G) ≥ d.
Upper Bound of X`(G)
To obtain an upper bound for X`(G), we note that if G has m edges, then X`(G) ≤ m.
However, this upper bound is very poor and has been improved by V. G. Vizing and C. E. Shannon.
Vizing's Theorem 4 If G is a simple graph whose maximum vertex-degree is d, then D ≤ X`(G) ≤ d+1. Following two theorems give upper bounds for the chromatic index of a graph with multiple edges.
Vizing's Theorem for Multiple Edges If G is a graph whose maximum vertex-degree is d, and if h is the maximum number of edges joining a pair of vertices, then d ≤ X`(G) ≤ d+h.
For example, consider the following graph in which d = 6 and h = 3.
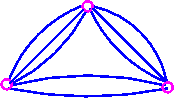
Therefore bounds are 6 ≤ X`(G) ≤ 9.
In fact, X`(G) = 8 for this particular graph.
Shannon's Theorem If G is a graph whose maximum vertex-degree is d, then d ≤ X`(G) ≤ 3/2 d.
For example, consider the following graph we have d = 6, and so bounds are 6 ≤ X`(G) ≤ 9. If d is odd, then (3/2)d is not an integer. In which case we can strengthen the bound to (3/2)d - 1/2.
We consider this section with an important theorem by Hungarian mathematician Denes Konig.
Konig's Theorem If G is n bipartite graph whose maximum vertex degree is d, then X`(G) = d.
Proof Idea Mathematical induction on the number of edge of G.
Konig's theorem tells us that every bipartite graph (not necessarily simple) with maximum vertex-degree d can be edge-colored with just d colors.
