A graph is an abstract notation used to represent the connection between pairs of objects. A graph consists of −

• Vertices − Interconnected objects in a graph are called vertices. Vertices are also known as nodes.

• Edges − Edges are the links that connect the vertices.

There are two types of graphs −

• Directed graph − In a directed graph, edges have direction, i.e., edges go from one vertex to another.

• Undirected graph − In an undirected graph, edges have no direction.

Graph Coloring

Graph coloring is a method to assign colors to the vertices of a graph so that no two adjacent vertices have the same color. Some graph coloring problems are −

• Vertex coloring − A way of coloring the vertices of a graph so that no two adjacent vertices share the same color.

• Edge Coloring − It is the method of assigning a color to each edge so that no two adjacent edges have the same color.

• Face coloring − It assigns a color to each face or region of a planar graph so that no two faces that share a common boundary have the same color.

Chromatic Number

Chromatic number is the minimum number of colors required to color a graph. For example, the chromatic number of the following graph is 3.

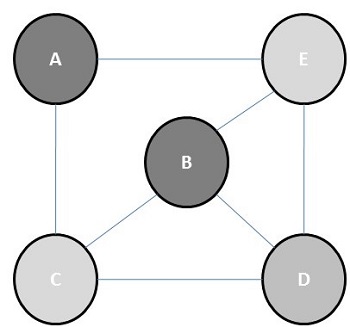
The concept of graph coloring is applied in preparing timetables, mobile radio frequency assignment, Suduku, register allocation, and coloring of maps.

Steps for graph coloring

• Set the initial value of each processor in the n-dimensional array to 1.

• Now to assign a particular color to a vertex, determine whether that color is already assigned to the adjacent vertices or not.

• If a processor detects same color in the adjacent vertices, it sets its value in the array to 0.

• After making n² comparisons, if any element of the array is 1, then it is a valid coloring.

Pseudocode for graph coloring

begin

   create the processors P(i0,i1,...in-1) where 0_iv < m, 0 _ v < n
   status[i0,..in-1] = 1
	
   for j varies from 0 to n-1 do
      begin
		
         for k varies from 0 to n-1 do
         begin
            if aj,k=1 and ij=ikthen
            status[i0,..in-1] =0
         end
			
      end
      ok = ΣStatus
		
   if ok > 0, then display valid coloring exists
   else
      display invalid coloring
      
end

Minimal Spanning Tree

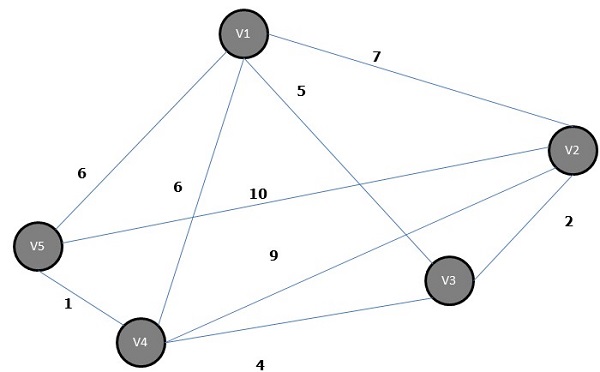
A spanning tree whose sum of weight (or length) of all its edges is less than all other possible spanning tree of graph G is known as a minimal spanning tree or minimum cost spanning tree. The following figure shows a weighted connected graph.

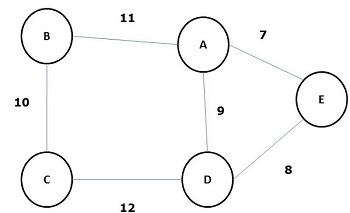
Some possible spanning trees of the above graph are shown below −

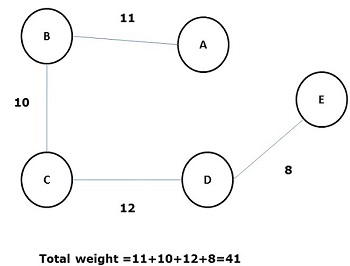
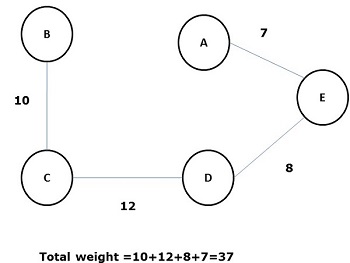
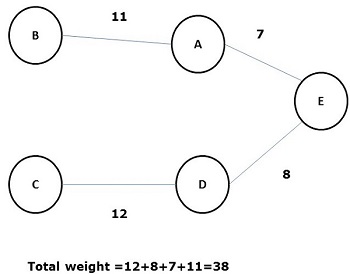
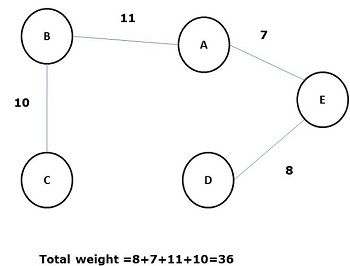
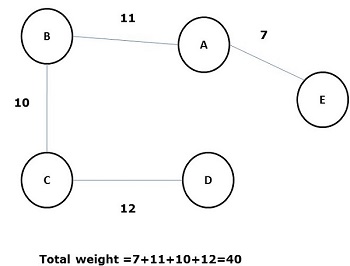
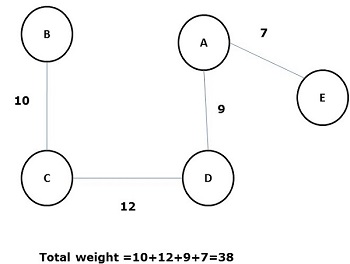
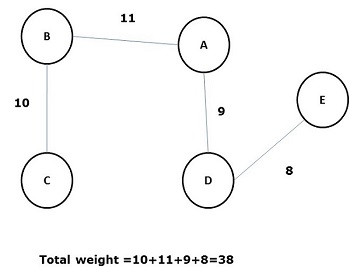
Among all the above spanning trees, figure (d) is the minimum spanning tree. The concept of minimum cost spanning tree is applied in travelling salesman problem, designing electronic circuits, Designing efficient networks, and designing efficient routing algorithms.

To implement the minimum cost-spanning tree, the following two methods are used −

• Prim’s Algorithm
• Kruskal’s Algorithm

Prim's Algorithm

Prim’s algorithm is a greedy algorithm, which helps us find the minimum spanning tree for a weighted undirected graph. It selects a vertex first and finds an edge with the lowest weight incident on that vertex.

Steps of Prim’s Algorithm

• Select any vertex, say v₁ of Graph G.

• Select an edge, say e₁ of G such that e₁ = v₁ v₂ and v₁ ≠ v₂ and e₁ has minimum weight among the edges incident on v₁ in graph G.

• Now, following step 2, select the minimum weighted edge incident on v₂.

• Continue this till n–1 edges have been chosen. Here n is the number of vertices.

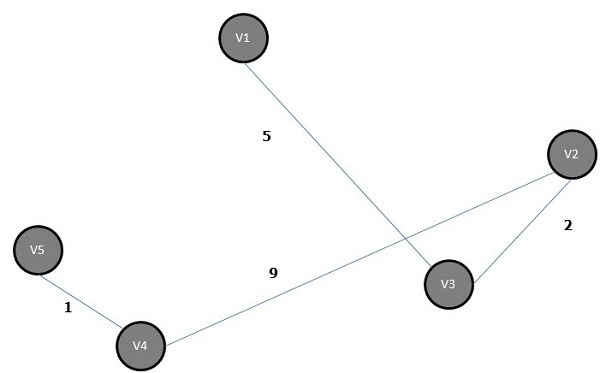
The minimum spanning tree is −

Kruskal's Algorithm

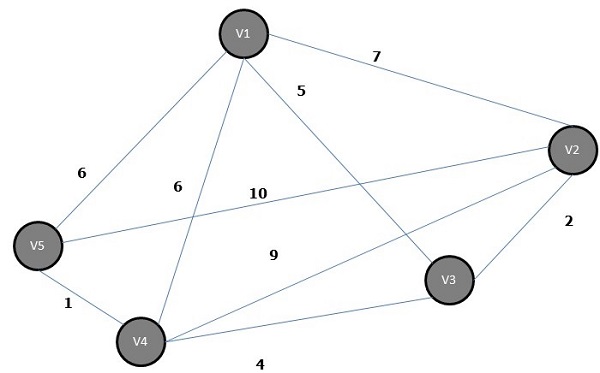
Kruskal’s algorithm is a greedy algorithm, which helps us find the minimum spanning tree for a connected weighted graph, adding increasing cost arcs at each step. It is a minimum-spanning-tree algorithm that finds an edge of the least possible weight that connects any two trees in the forest.

Steps of Kruskal’s Algorithm

• Select an edge of minimum weight; say e₁ of Graph G and e₁ is not a loop.

• Select the next minimum weighted edge connected to e₁.

• Continue this till n–1 edges have been chosen. Here n is the number of vertices.

The minimum spanning tree of the above graph is −

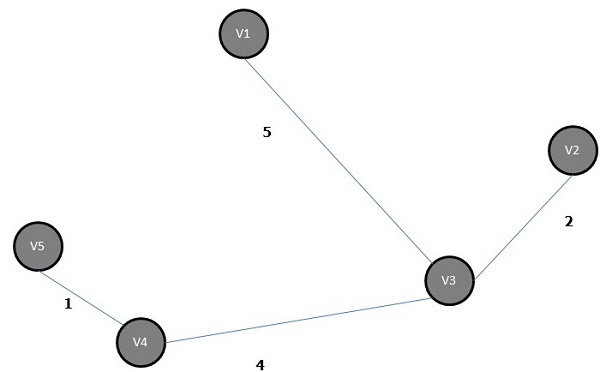
Shortest Path Algorithm

Shortest Path algorithm is a method of finding the least cost path from the source node(S) to the destination node (D). Here, we will discuss Moore’s algorithm, also known as Breadth First Search Algorithm.

Moore’s algorithm

• Label the source vertex, S and label it i and set i=0.

• Find all unlabeled vertices adjacent to the vertex labeled i. If no vertices are connected to the vertex, S, then vertex, D, is not connected to S. If there are vertices connected to S, label them i+1.

• If D is labeled, then go to step 4, else go to step 2 to increase i=i+1.

• Stop after the length of the shortest path is found.