A source code can directly be translated into its target machine code, then why at all we need to translate the source code into an intermediate code which is then translated to its target code? Let us see the reasons why we need an intermediate code.
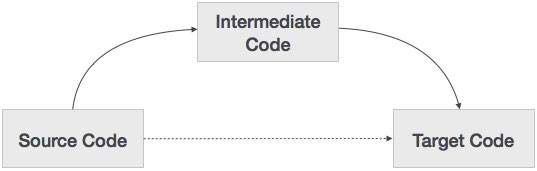
If a compiler translates the source language to its target machine language without having the option for generating intermediate code, then for each new machine, a full native compiler is required.
Intermediate code eliminates the need of a new full compiler for every unique machine by keeping the analysis portion same for all the compilers.
The second part of compiler, synthesis, is changed according to the target machine.
It becomes easier to apply the source code modifications to improve code performance by applying code optimization techniques on the intermediate code.
Intermediate Representation
Intermediate codes can be represented in a variety of ways and they have their own benefits.
High Level IR - High-level intermediate code representation is very close to the source language itself. They can be easily generated from the source code and we can easily apply code modifications to enhance performance. But for target machine optimization, it is less preferred.
Low Level IR - This one is close to the target machine, which makes it suitable for register and memory allocation, instruction set selection, etc. It is good for machine-dependent optimizations.
Intermediate code can be either language specific (e.g., Byte Code for Java) or language independent (three-address code).
Three-Address Code
Intermediate code generator receives input from its predecessor phase, semantic analyzer, in the form of an annotated syntax tree. That syntax tree then can be converted into a linear representation, e.g., postfix notation. Intermediate code tends to be machine independent code. Therefore, code generator assumes to have unlimited number of memory storage (register) to generate code.
For example:
a = b + c * d;
The intermediate code generator will try to divide this expression into sub-expressions and then generate the corresponding code.
r1 = c * d; r2 = b + r1; a = r2
r being used as registers in the target program.
A three-address code has at most three address locations to calculate the expression. A three-address code can be represented in two forms : quadruples and triples.
Quadruples
Each instruction in quadruples presentation is divided into four fields: operator, arg1, arg2, and result. The above example is represented below in quadruples format:
| Op | arg1 | arg2 | result |
| * | c | d | r1 |
| + | b | r1 | r2 |
| + | r2 | r1 | r3 |
| = | r3 | a |
Triples
Each instruction in triples presentation has three fields : op, arg1, and arg2.The results of respective sub-expressions are denoted by the position of expression. Triples represent similarity with DAG and syntax tree. They are equivalent to DAG while representing expressions.
| Op | arg1 | arg2 |
| * | c | d |
| + | b | (0) |
| + | (1) | (0) |
| = | (2) |
Triples face the problem of code immovability while optimization, as the results are positional and changing the order or position of an expression may cause problems.
Indirect Triples
This representation is an enhancement over triples representation. It uses pointers instead of position to store results. This enables the optimizers to freely re-position the sub-expression to produce an optimized code.
Declarations
A variable or procedure has to be declared before it can be used. Declaration involves allocation of space in memory and entry of type and name in the symbol table. A program may be coded and designed keeping the target machine structure in mind, but it may not always be possible to accurately convert a source code to its target language.
Taking the whole program as a collection of procedures and sub-procedures, it becomes possible to declare all the names local to the procedure. Memory allocation is done in a consecutive manner and names are allocated to memory in the sequence they are declared in the program. We use offset variable and set it to zero {offset = 0} that denote the base address.
The source programming language and the target machine architecture may vary in the way names are stored, so relative addressing is used. While the first name is allocated memory starting from the memory location 0 {offset=0}, the next name declared later, should be allocated memory next to the first one.
Example:
We take the example of C programming language where an integer variable is assigned 2 bytes of memory and a float variable is assigned 4 bytes of memory.
int a;
float b;
Allocation process:
{offset = 0}
int a;
id.type = int
id.width = 2
offset = offset + id.width
{offset = 2}
float b;
id.type = float
id.width = 4
offset = offset + id.width
{offset = 6}
To enter this detail in a symbol table, a procedure enter can be used. This method may have the following structure:
enter(name, type, offset)
This procedure should create an entry in the symbol table, for variable name, having its type set to type and relative address offset in its data area.
